Что такое четырехугольник: основы геометрии

Четырехугольник - одна из самых распространенных геометрических фигур. Мы встречаем четырехугольники повсюду: рамки картин, окна и двери в домах, столы, парты в школе и многое другое имеет форму четырехугольника. Давайте разберемся, что это такое.

Определение четырехугольника

Итак, что такое четырехугольник? Четырехугольник - это геометрическая фигура, образованная четырьмя точками, которые называются вершинами, и четырьмя отрезками, которые называются сторонами.

Четырехугольник состоит из:

• 4 вершин
• 4 сторон
• 4 углов

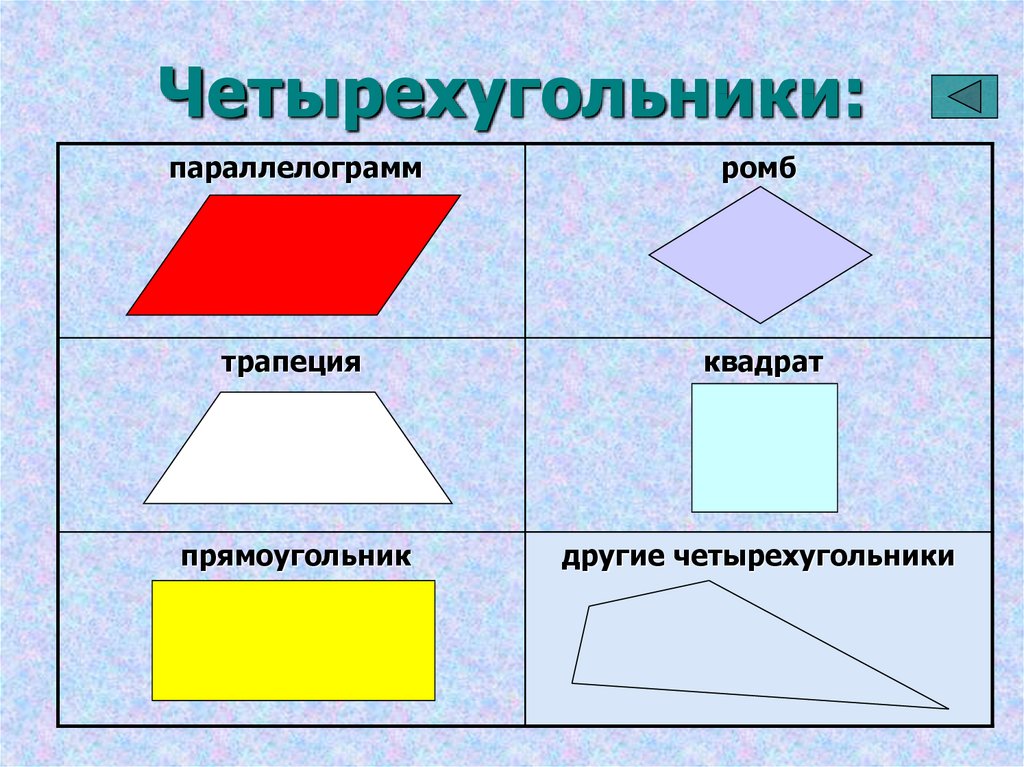
Существуют разные типы четырехугольников:

1. Выпуклые - у которых все углы меньше 180 градусов
2. Невыпуклые - у которых есть угол больше 180 градусов
3. Самопересекающиеся - у которых стороны пересекаются

У every четырехугольника есть общие свойства:

• Сумма всех углов = 360 градусов
• Сумма длин любых трех сторон больше длины четвертой стороны

Четырехугольники часто встречаются в окружающем мире: рамы, картины... Теперь давайте разберем, на какие виды делятся четырехугольники и чем они отличаются.

Существует много разных видов четырехугольников. Рассмотрим основные.

Трапеция

Трапеция - это четырехугольник, у которого две стороны параллельны. Например, футбольное поле имеет форму трапеции.

Параллелограмм

Параллелограмм - четырехугольник, у которого противоположные стороны параллельны. К параллелограммам относятся:

• Прямоугольник
• Ромб
• Квадрат

У этих фигур есть общие и отличительные свойства. Например, у всех параллелограммов противоположные стороны и углы равны. А квадрат - это прямоугольник, у которого все стороны равны.

Кроме того, существуют дельтоид, антипараллелограмм и другие интересные виды четырехугольников.

Свойства параллелограмма

У параллелограмма есть уникальные свойства, отличающие его от других четырехугольников:

• Противоположные стороны и углы равны
• Диагонали взаимно перпендикулярны (для некоторых видов параллелограмма)
• Диагонали пересекаются в точке, делящей их пополам

Эти свойства позволяют отличить параллелограмм от трапеции или произвольного четырехугольника.

Формулы площади

Что такое площадь четырехугольника? Это мера того, сколько места занимает четырехугольник на плоскости.

Для разных видов четырехугольников существуют свои формулы площади:

• Параллелограмм: S = a * h
• Трапеция: S = (a + b) * h / 2
• Прямоугольник: S = a * b

Где: S - площадь, a и b - основания, h - высота.

Задачи на четырехугольники

Рассмотрим примеры задач на четырехугольники.

1. Найти площадь квадрата со стороной 5 см
2. В трапеции основания равны 8 см и 12 см, а высота равна 5 см. Найти площадь трапеции.

Такие задачи решаются подстановкой значений в известные формулы. Давайте разберем решение подробно.

Геометрические построения

Помимо вычисления площадей, важно уметь выполнять различные геометрические построения с четырехугольниками.

• Построение средних линий
• Построение биссектрис
• Вписывание и описывание окружностей

Пример задачи на площадь квадрата

Дано: сторона квадрата а = 5 см.

Формула площади квадрата: S = a²

Подставляем значение стороны в формулу: S = 5² = 25 см²

Ответ: площадь квадрата со стороной 5 см равна 25 см².

Задача на площадь трапеции

Дано:

• Основание а = 8 см
• Основание b = 12 см
• Высота h = 5 см

Формула площади трапеции: \

S = (a + b) * h / 2

Вычисляем:

S = (8 + 12) * 5 / 2 = 10 * 5 = 50 см²

Ответ: Площадь трапеции равна 50 см².

Алгоритм построения биссектрисы четырехугольника

Чтобы построить биссектрису угла четырехугольника:

1. Строим четырехугольник ABC
2. Выбираем угол, например B
3. Радиус-вектором строим дуги, отсекающие равные отрезки BC и BA
4. Соединяем точки пересечения дуг - получаем биссектрису угла В

Описание четырехугольника окружностью

Четырехугольник можно описать окружностью, которая проходит через все его вершины. Для этого:

1. Строим четырехугольник ABCD
2. Строим серединные перпендикуляры ко всем сторонам четырехугольника
3. Находим точку пересечения серединных перпендикуляров - это центр описанной окружности
4. Проводим окружность радиусом, равным расстоянию от центра до любой вершины

Таким образом получаем окружность, описанную около четырехугольника.

Задачи на вычисление углов четырехугольника

Помимо площади, в задачах часто приходится вычислять углы четырехугольника. Например:

Углы четырехугольника относятся как 2:3:4:5. Найти величину каждого угла.

Решение:

1. Обозначим углы: α, β, γ, δ
2. Составляем пропорцию из условия задачи
3. Используем свойство, что сумма углов четырехугольника = 360°
   

Свойства четырехугольника в геометрических задачах

Для доказательства геометрических утверждений о четырехугольнике используют такие его свойства, как:

• Сумма углов четырехугольника равна 360°
• Сумма квадратов диагоналей равна сумме квадратов сторон (для выпуклых четырехугольников)