Параллелограмм и его свойства: полное руководство

Геометрия - один из самых сложных и в то же время интересных разделов школьной программы. От умения решать геометрические задачи во многом зависит успешная сдача ЕГЭ и поступление в вуз. Но что делать, если кажется, что все формулы и теоремы перепутались и никак не хотят складываться в голове? Не отчаивайтесь! В этой статье мы подробно разберем одну из базовых тем - параллелограмм и его свойства.

История и этимология понятия "параллелограмм"

Термин «параллелограмм» имеет древнегреческое происхождение. Согласно древнегреческому философу Проклу, он был введен Евклидом. Впервые это понятие упоминается в труде Евклида «Начала», где доказывается, что в параллелограмме диагональ делит его пополам.

Само слово «параллелограмм» составлено из двух греческих слов: «параллелос» - параллельный и «грамме» - линия. Таким образом, дословный перевод означает «параллельные линии».

Полная теория параллелограммов сложилась лишь к концу Средних веков. Понятие и некоторые свойства параллелограмма были известны еще пифагорейцам. Они связывали фигуру ромба с вращающимися предметами – юлой или веретеном.

Основные понятия и определения

Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. У него есть три основных признака:

• Противоположные стороны параллельны
• Противоположные стороны равны
• Диагонали взаимно пересекаются в точке пересечения и делятся этой точкой пополам

Из определения вытекает ряд важных свойств параллелограмма:

1. Противоположные углы равны
2. Сумма углов прилежащих к одной стороне равна 180°
3. Диагонали делят параллелограмм на два равных треугольника
4. Биссектриса угла отсекает равнобедренный треугольник
5. Биссектрисы противоположных углов параллельны

Различают несколько видов параллелограммов:

• Прямоугольник
• Ромб
• Квадрат

Они являются частными случаями и обладают дополнительными свойствами. Например, у ромба диагонали взаимно перпендикулярны, а у прямоугольника диагонали равны.

В окружающем мире параллелограммы часто встречаются: рамы картин и окон, двери, столы и многое другое имеют форму параллелограмма.

Построение и вычисление параметров

Для построения параллелограмма по известным параметрам можно использовать несколько методов. Рассмотрим один из них:

1. Провести одну сторону AB произвольной длины
2. Из точки B провести линию BC под заданным углом α к AB
3. Из точки C опустить перпендикуляр CD на AB
4. Получить точку D так, чтобы отрезок AD был равен BC
5. Соединить точки C и D

Для нахождения площади параллелограмма используется формула S=ah, где a - длина стороны, h - высота, проведенная к этой стороне.

Другая формула для вычисления площади: S=1/2(AB x BC), где AB и BC - стороны параллелограмма.

Чтобы найти углы параллелограмма, можно воспользоваться его свойством: противоположные углы равны. Зная величину одного угла, легко определить остальные.

Биссектрисы и диагонали

Биссектриса параллелограмма делит его внутренний угол пополам. При этом выполняется два важных свойства:

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Биссектрисы противоположных углов параллелограмма параллельны.

Эти утверждения можно строго доказать с помощью теорем и определений.

Что касается диагоналей параллелограмма, то для них справедлива следующая теорема:

Диагонали параллелограмма делят его на два равных треугольника.

Доказательство опирается на то, что диагонали пересекаются в середине, а стороны параллелограмма равны.

Применение свойств параллелограмма в задачах ЕГЭ

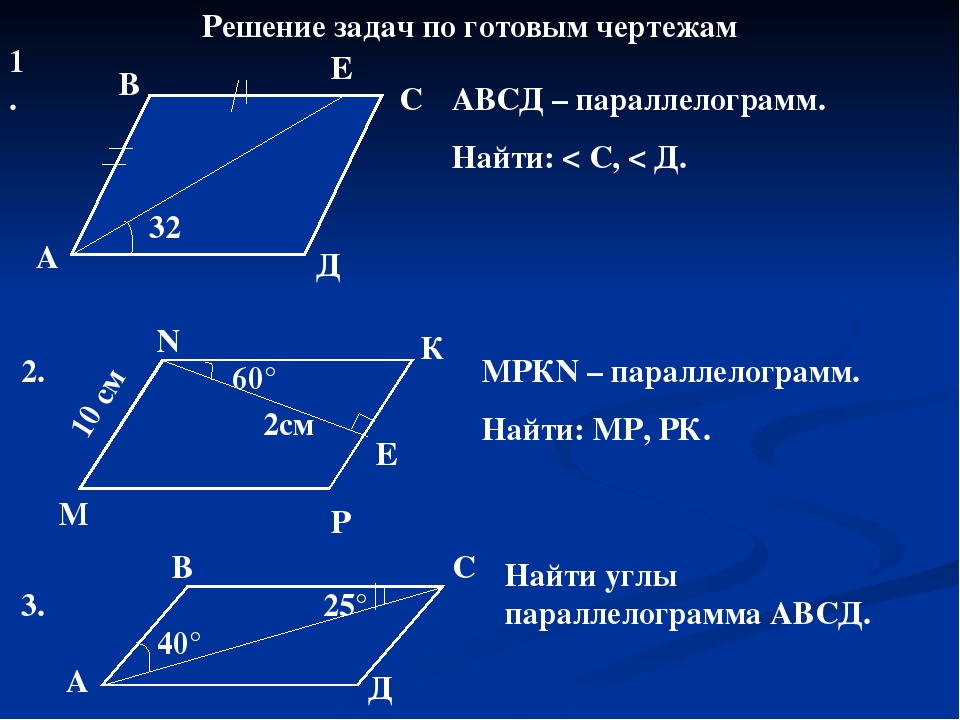
Знание свойств параллелограмма очень полезно для решения задач ЕГЭ по геометрии. Рассмотрим несколько примеров.

Задача: найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне.

Решение: используем свойство - биссектрисы соседних углов параллелограмма перпендикулярны. Следовательно, искомый угол равен 90°.

Построение параллелограмма по заданным элементам

Часто в заданиях ЕГЭ требуется построить параллелограмм, если даны некоторые его элементы: стороны, углы, высоты и т.д. Рассмотрим алгоритм выполнения такого построения.

1. Если заданы две стороны и угол между ними, строим треугольник
2. Через одну из вершин треугольника проводим параллельную его сторону
3. Получаем искомый параллелограмм

Данный метод опирается на признак параллелограмма: наличие параллельных и равных противоположных сторон.