Уравнение: что это такое, методы решения

Уравнения являются одним из фундаментальных математических понятий, без которого невозможно представить современную науку. Их изучают еще в начальной школе, а затем применяют на протяжении всей жизни – от решения бытовых задач до описания сложных физических процессов.

Что такое уравнение

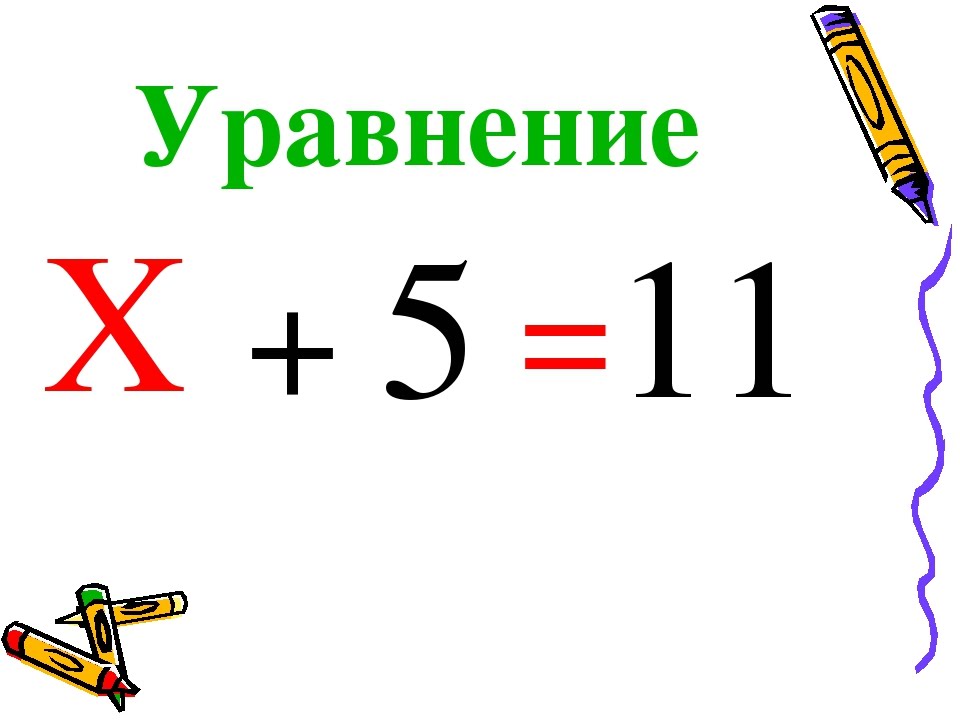
Уравнение – это математическое выражение, содержащее неизвестное значение, обозначаемое обычно буквой. Цель решения уравнения – найти такое конкретное число, при подстановке которого вместо этой буквы равенство обратится в верное числовое тождество. Это число называется корнем уравнения.

Например, рассмотрим линейное уравнение первой степени:

5x + 7 = 27

Здесь x – неизвестное число. Чтобы решить это уравнение, нужно выполнить ряд преобразований и в итоге получить:

x = 4

Значит, корень данного уравнения равен 4. Проверим:

5 ∙ 4 + 7 = 20 + 7 = 27

Действительно, подставив 4 вместо x, мы получили верное числовое равенство. Значит, число 4 является решением нашего уравнения.

Основные типы уравнений

Различают несколько основных типов уравнений:

• Линейные уравнения, в которых неизвестное стоит только в первой степени.
• Квадратные уравнения, где неизвестное возведено в квадрат.
• Дробно-рациональные уравнения, содержащие дробные выражения.
• Иррациональные уравнения с корнями и другими иррациональными операциями.
• Показательные и логарифмические уравнения.
• Тригонометрические уравнения с trig-функциями.

Также различают уравнение с одним неизвестным и системы уравнений, где одновременно нужно находить значения нескольких переменных.

Значение уравнений в науке и технике

Уравнения широко используются во всех областях точных и естественных наук. Они позволяют устанавливать количественные зависимости между различными величинами и делать полезные выводы об окружающем мире. Большинство физических законов формулируются именно как уравнения.

Например, одним из фундаментальных уравнений - это уравнение Эйнштейна E = mc2, которое устанавливает связь между энергией, массой и скоростью света. А уравнение реакции фотосинтеза описывает процесс преобразования углекислого газа и воды в органические вещества:

CO2 + H2O → C6H12O6 + O2↑

Решая химические и физические уравнение реакции, можно рассчитать скорость реакции, выход продукта, оптимальные условия проведения процесса.

В инженерии уравнениями описывают работу технических устройств, напряженно-деформированное состояние конструкций, тепловые и гидродинамические процессы. Это позволяет строить надежные модели и прогнозировать поведение сложных систем.

Таким образом, значение уравнений в науке и технике трудно переоценить. Фактически они являются универсальным языком, на котором описываются количественные взаимосвязи в природе и обществе.

Алгоритм решение уравнений

Рассмотрим общий алгоритм решите уравнение на примере линейного уравнения с одной переменной:

1. Записать уравнение, выделив неизвестное число.
2. Выполнить необходимые математические преобразования обеих частей уравнения, чтобы получить неизвестное в отдельности.
3. Найти числовое значение этого неизвестного – это и будет корень уравнения.
4. Подставить корень обратно в уравнение, убедиться, что получилось верное равенство.

Например:

1. 4(x + 1) = 28
2. 4x + 4 = 28
3. 4x = 24
4. x = 6
5. Проверка: 4(6 + 1) = 4∙7 = 28 – верно.

Таким образом, мы нашли решение уравнения x = 6.

Системы уравнений

Если одного уравнения недостаточно для нахождения неизвестных в задаче, используют система уравнений. Система состоит из двух и более уравнений с двумя или более переменными. Решением системы являются такие числовые значения переменных, которые одновременно удовлетворяют всем уравнениям.

Например, чтобы найти цены яблок и груш, можно составить систему из двух уравнений:

2x + 3y = 42
4x + 2y = 44

Здесь x – цена яблок (за 1 кг), а y – цена груш (за 1 кг). Решив эту систему, получаем:

x = 6 руб. y = 10 руб.

Итак, яблоки стоят 6 рублей за 1 кг, а груши – 10 рублей за 1 кг.

Системы уравнений часто применяются в экономике и технике для моделирования сложных процессов с несколькими переменными.

Методы решения уравнений

Для решения различных типов уравнений используются как аналитические, так и численные методы. Рассмотрим некоторые из них.

Аналитические методы

К уравнениям, которые можно решить в «закрытом» аналитическом виде, относятся линейные, квадратные, показательные, логарифмические, тригонометрические. Для них существуют общие формулы нахождения корней.

Например, для квадратного уравнения ax^2 + bx + c = 0 известна формула корней, выведенная еще в Древнем Вавилоне:

x1,2 = (-b ± √(b^2-4ac)) / 2a

Подставив коэффициенты a, b и c, можно найти численное значение корней.

Численные методы

Если аналитического решения уравнение не имеет, применяют численные методы – последовательное приближение к корню с заданной точностью. Наиболее распространены:

• Метод деления отрезка пополам
• Метод касательных
• Метод итераций
• Метод Ньютона

Эти методы широко используются при решении уравнений в вычислительной математике и программировании.

Графический метод решения

Еще один подход – построение графика функции и нахождение точек ее пересечения с осью X. Абсциссы этих точек и будут корнями уравнения.

Например:

Графический метод удобен для приближенного нахождения корней, нагляден, не требует вычислений.

Практическое применение уравнений

Кроме теоретических исследований, уравнения активно используют в инженерных расчетах, экономическом планировании, оптимизации производства и других прикладных областях.

Технические расчеты

С помощью уравнений описывают работу электрических цепей, механических и гидравлических систем, теплообмен в конструкциях. Это позволяет точно моделировать физические процессы и оптимизировать конструкции.

Экономика и финансы

В экономике уравнениями задают функции спроса и предложения, описывают динамику спроса от цены, моделируют рыночное равновесие. С их помощью анализируют экономическую эффективность инвестиций.

В финансовой сфере уравнения применяют для анализа кредитных рисков, оптимизации инвестиционного портфеля, оценки стоимости активов.

Занимательные факты об уравнениях

• Самое длинное уравнение в мире – уравнение гравитационного поля квантовой струны, содержащее более 500 000 знаков!
• У легендарного математика Рамануджана не было формального образования. Но в 16 лет он самостоятельно открыл много оригинальных формул для решения уравнений.
• Древние вавилоняне умели решать квадратные уравнения еще 4 тысячи лет назад, задолго до открытия алгебры.