Комплексные числа и действия над ними

Автор Юлия Петрук June 29, 2015

Комплексные числа, в традиционном смысле этого слова, не являются числами, применяемыми при подсчетах и измерениях, а являются математическими объектами, которые определяются представленными ниже свойствами.

Используют 3 формы комплексного числа: алгебраическую, показательную, тригонометрическую.

Форма алгебраическая

Комплексные числа обозначают выражением ω + νi, где действительными являются ω и ν, а символ i, определяется условием i² - 1 - единица мнимая.

Соответственно число комплексное ω + νi делится на действительную и мнимую часть. Для удобства изображают его одной буквой (например η): η = ω + νi.

Части числа комплексного η = ω + νi, действительную и мнимую, обозначают ω = Reη, ν = Itη соответственно.

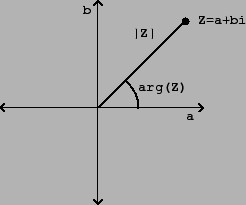
Равными считаются комплексные числа, когда эквивалентны их и действительные и мнимые части. Равным нулю считается комплексное число, если его части, действительная и мнимая, равны нулю.

Арифметические действия

Сложение

Суммой комплексных чисел именуют число комплексное, действительная часть которого эквивалентна сумме действительных частей, а мнимая эквивалентна сумме мнимых частей:

η=(ω₁+ω₂)+(ν₁+ν₂)i.

Говорят что в числе комплексном η обрели в результате сложения чисел комплексных:

η=η₁+η_2.

Комплексные η₁ и η₂ именуют слагаемыми.

Законы операции сложения:

1) закон ассоциативности;

2) закон коммутативности.

Число комплексное -ω-bi называют комплексному числу ω+νi противоположным. Сумма противоположных комплексных чисел равняется нулю.

Разница

Разницей чисел комплексных называют число комплексное η равное сумме числа η₁ и числа противоположного η₂:

η=η₁+(-η₂)=(ω₁-ω₂)+(ν₁-ν₂)i.

О числе комплексном η говорят, что его обрели в результате вычитания η₂ и η₁(чисел комплексных), и записывают:

η=η₂-η₁.

Произведение

Произведением чисел комплексныхявляется число комплексное:

η=(ω₁ω₂-ν₁ν₂)+(ω₁ν₁+ω₂ν₁)i.

О числе комплексном η говорят, что его получили умножением η₁ на η₂(числа η₁ и η₂ - комплексные), и записывают:

η=η₁η₂.

Комплексные η₁ и η₂именуют множителями.

Законы операции умножения чисел комплексных:

1) закон ассоциативности;

2) закон коммутативности.

Деление

Частным чисел комплексных называют такое комплексное η, что η₁=η_1:η₂(η2 ≠ 0). Частное чисел комплексных вычисляют по формуле:

η=(ω₁ω₂-ν₁ν₂)/(ω²+ν²)+(ω₁ν₁+ ω₂ ν₁)i/(ω²+ ν²).

О числе η говорят, что его получили в результате деления η₁ на η₂, и записывают:

η=η₁/η₂_.

Сложение и умножение чисел комплексных связаны правилом, которое называется дистрибутивным законом умножения касательно сложения.

Тригонометрические комплексные числа

Применяют также другую форму записи чисел комплексных, которая называется тригонометрической.

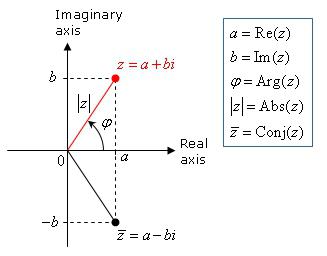
Число комплексное ω + νi записать можно так:

η=k(cosβ+isinβ), где k²=ω²+ν².

Это выражение - форма записи чисел комплексных, которая носит название тригонометрической. Модуль числа комплексного - действительное число k, а угол β, измеренный в радианах - его аргументом.

Если число комплексное не равно нулю, то модуль его положительный; если же η=0, иначе говоря ω=ν=0, то и модуль его равен нулю. Модуль определен однозначно.

Произведением тригонометрических комплексных чисел является модуль числа комплексного, который эквивалентен произведению множителей, вернее, их модулей, а аргумент эквивалентен сумме аргументов множителей:

η₁η₂=k₁k₂[cos(β₁+β₂)+isin(β₁+β₂)].

Частным тригонометрических комплексных чисел, которые не равны нулю, является число комплексное, модуль которого эквивалентен частному делимого и делителя (их модулей), а аргумент эквивалентен разнице аргументов делимого и делителя:

η₁/η₂=k₁/k₂[cos(β₁-β₂)+isin(β₁-β₂)].