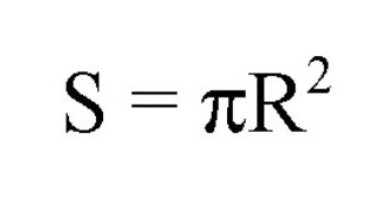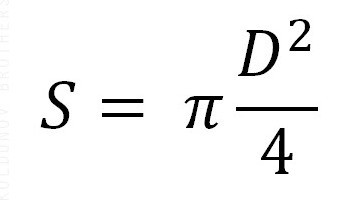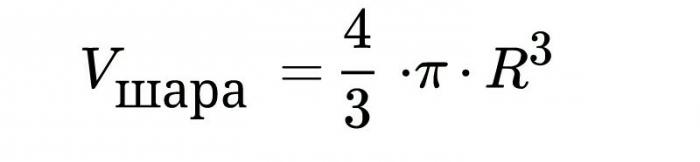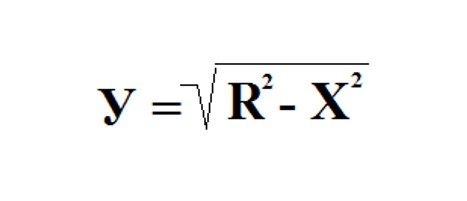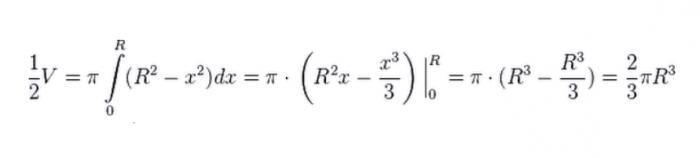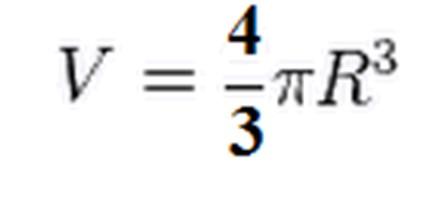Как вычислить объем шара и другие нюансы при вычислениях

Прежде чем начать изучать понятие шара, что такое объём шара, рассматривать формулы исчисления его параметров, необходимо вспомнить о понятии круга, изучаемом ранее в курсе геометрии. Ведь большинство действий в трехмерном пространстве аналогичны или вытекают из двумерной геометрии с поправкой на появление третьей координаты и третьей степени.

Что такое круг?

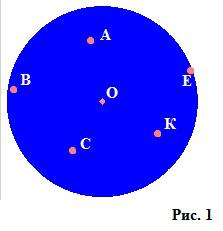
Круг – это фигура на декартовой плоскости (изображена на рисунке 1); наиболее часто определение звучит как «геометрическое место всех точек на плоскости, расстояние от которых до заданной точки (центра) не превышает некоего неотрицательного числа, называемого радиусом».

Как видим по рисунку, точка О – это центр фигуры, а множество абсолютно всех точек, что заполняют круг, к примеру, А, В, С, К, Е, находятся не далее заданного радиуса (не выходят за пределы окружности, изображенной на рис. 2).

Если радиус равен нулю, то круг превращается в точку.

Проблемы с пониманием

Ученики часто путают эти понятия. Легко запомнить, проведя аналогию. Обруч, который дети крутят на уроках физической культуры, – окружность. Понимая это или запомнив, что первые буквы обоих слов – "О", дети мнемонически будут понимать разницу.

Введение понятия «шар»

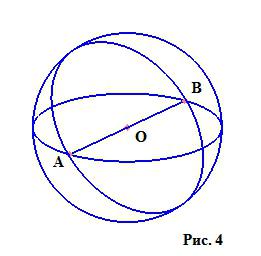
Шар – это тело (рис. 3), ограниченное некой сферической поверхностью. Что за «сферическая поверхность», станет ясно из ее определения: это геометрическое место всех точек на поверхности, расстояние от которых до заданной точки (центра) не превышает некоего неотрицательного числа, называемого радиусом. Как видим, понятия круга и сферической поверхности аналогичны, только разнятся пространства, в которых они находятся. Если изобразить шар в двумерном пространстве, мы получаем круг, границей которого является окружность (у шара граница – сферическая поверхность). На рисунке мы видим сферическую поверхность с радиусами ОА = ОВ.

Шар замкнутый и открытый

В векторном и метрическом пространствах также рассматриваются два понятия, связанные со сферической поверхностью. Если шар включает эту сферу в себя, то он называется замкнутым, а если же нет, то в таком случае шар является открытым. Это более "продвинутые" понятия, их изучают в институтах при введении в анализ. Для простого, даже бытового использования будет достаточно и тех формул, которые изучаются в курсе стереометрии 10-11 классов. Именно такие, доступные практически каждому среднестатистическому образованному человеку понятия будут рассмотрены далее.

Понятия, которые нужно знать для следующих вычислений

- Радиус и диаметр.

- Радиус шара и его диаметр определяются так же, как у круга.

- Радиус – отрезок, соединяющий любую точку на границе шара и точку, являющуюся центром шара.

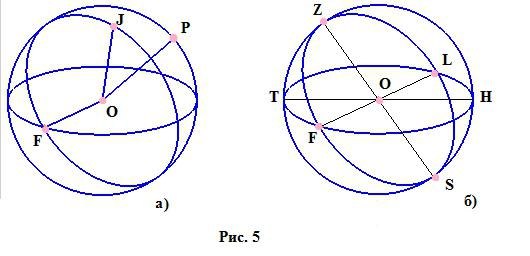
- Диаметр – отрезок, соединяющий две точки на границе шара и проходящий через его центр. Рисунок 5а наглядно демонстрирует, какие отрезки являются радиусами шара, а на рисунке 5б изображены диаметры сферы (отрезки, проходящие через точку О).

Сечения в сфере (шаре)

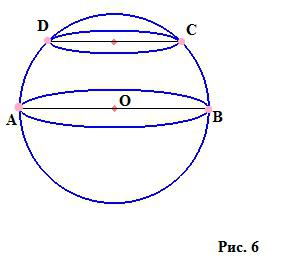
Любое сечение сферы является кругом. Если оно проходит через центр шара, то называется большим кругом (окружность с диаметром АВ), остальные сечения – малыми кругами (окружность с диаметром DC).

Площадь данных кругов вычисляется по следующим формулам:

Здесь S – это обозначение площади, R – радиуса, D – диаметра. Также присутствует константа, равная 3,14. Но не стоит путать, что для исчисления площади большого круга используют радиус или диаметр самого шара (сферы), а для определения площади требуются размеры радиуса именно малой окружности.

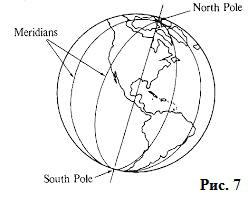
Таких сечений, которые проходят через две точки одного диаметра, лежащих на границе шара, можно провести бесчисленное число. Как пример – наша планета: две точки на Северном и Южном полюсах, которые являются концами земной оси, а в геометрическом смысле – концами диаметра, и меридианы, которые проходят через эти две точки (рисунок 7). То есть число больших кругов у сферы по количеству стремится к бесконечности.

Части шара

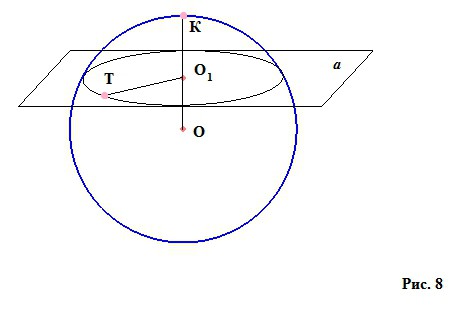
Если отсечь от сферы при помощи некоторой плоскости «кусочек» (рисунок 8), то он будет называться сферическим или шаровым сегментом. У него будет высота – перпендикуляр из центра секущей плоскости до сферической поверхности О₁К. Точка К на сферической поверхности, в которую приходит высота, называется вершиной сферического сегмента. А малый круг с радиусом О₁Т (в данном случае, согласно с рисунком, плоскость не прошла через центр сферы, но если сечение будет проходить через центр, то круг сечения будет большим), образованный при отсечении шарового сегмента, будет называться основанием нашего кусочка шара – сферического сегмента.

Если соединить каждую точку основания сферического сегмента с центром сферы, мы получим фигуру под названием "шаровой сектор".

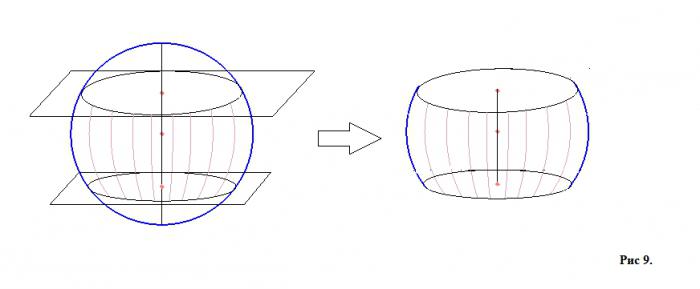
Если через сферу проходят две плоскости, которые между собой параллельны, то та часть сферы, которая заключена между ними, называется шаровым слоем (рисунок 9, где изображена сфера с двумя плоскостями и отдельно – шаровой слой).

Поверхность (выделенная часть на рисунке 9 справа) этой части сферы называется поясом (снова для лучшего понимания можно провести аналогию с земным шаром, а именно с его климатическими поясами – арктическими, тропическими, умеренными и т. д.), а круги сечения будут основаниями шарового слоя. Высота слоя – часть диаметра, проведённого перпендикулярно к секущим плоскостям из центров оснований. Существует также понятие шаровой сферы. Она образуется в том случае, когда плоскости, которые параллельны друг другу, не пересекают сферу, а касаются ее в одной точке каждая.

Формулы исчисления объёма шара и площади его поверхности

Шар образуется при вращении вокруг неподвижного диаметра полукруга или круга. Для вычислений разных параметров данного объекта понадобится не так уж много данных.

Объем шара, формула для исчисления которого указана выше, выведен посредством интегрирования. Разберемся по пунктам.

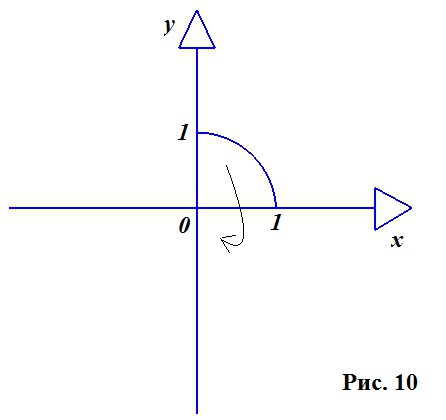
Рассматриваем круг в двумерной плоскости, ведь, как было сказано выше, именно круг лежит в основе построения шара. Используем лишь его четвертую часть (рисунок 10).

Берем круг с единичным радиусом и центром в начале координат. Уравнение такого круга выглядит следующим образом: Х² + У² = R². Выражаем отсюда У: У² = R² - Х².

Обязательно отметим, что полученная функция неотрицательная, непрерывная и убывающая на отрезке Х (0; R), ведь значение Х в том случае, когда мы рассматриваем четверть круга, лежит от нуля до значения радиуса, то есть до единицы.

Следующее, что мы делаем, это вращаем нашу четверть круга вокруг оси абсцисс. В результате мы получим полушар. Чтобы определить его объём, прибегнем к методам интегрирования.

Так как это объём лишь полушара, увеличиваем результат в два раза, откуда получаем, что объем шара равен:

Мелкие нюансы

Если необходимо вычислить объем шара через его диаметр, помним о том, что радиус – это половина диаметра, и подставляем это значение в вышеуказанную формулу.

Также к формуле объема шара можно дойти через площадь его граничащей поверхности – сферы. Напомним, что площадь сферы вычисляется по формуле S = 4πr², проинтегрировав которую, также придем к вышеуказанной формуле объема шара. Из этих же формул можно выразить радиус, если в условии задачи есть значение объема.