Объем конуса, его расчет

Геометрия как наука сформировалась в Древнем Египте и достигла высокого уровня развития. Известный философ Платон основал Академию, где пристальное внимание уделялось систематизации имеющихся знаний. Конус как одна из геометрических фигур впервые упоминается в известном трактате Евклида "Начала". Евклид был знаком с трудами Платона. Сейчас мало кто знает, что слово "конус" в переводе с греческого языка обозначает "сосновая шишка". Греческий математик Евклид, живший в Александрии, по праву считается основоположником геометрической алгебры. Древние греки не только стали преемниками знаний египтян, но и значительно расширили теорию.

История определения конуса

Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.

В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.

Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.

Основные определения

Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.

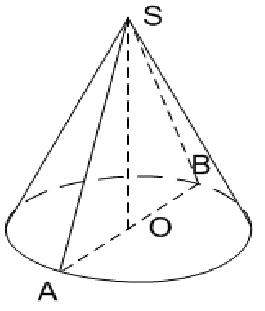
Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.

Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.

Также часто требуется рассчитать площадь боковой поверхности тела вращения. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

S=C*L/2=n*R*L/2

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Формула расчета объема конуса

Для расчета объема конуса используется следующая формула:

V=S*H/3,

где S является площадью основания конуса. Так как основание — круг, его площадь рассчитывается так:

S=nR².

Отсюда следует:

V=n*R²*H/3,

где V — объем конуса;

n — число, равное 3,14;

R — радиус основания, соответствующий отрезку AO на рисунке 1;

H — высота, равная отрезку OS.

Усеченный конус, объем

Имеется прямой круговой конус. Если плоскостью, перпендикулярной высоте, отсечь верхнюю часть, то получится усеченный конус. Два его основания имеют форму круга с радиусами R₁ и R₂.

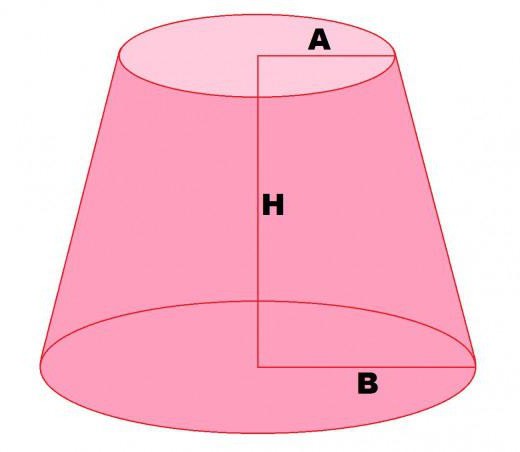
R₁=A;

R₂=B;

H=H.

Если прямой конус образуется вращением прямоугольного треугольника, то усеченный конус — вращением прямоугольной трапеции вокруг прямой стороны.

Объем усеченного конуса рассчитывается по следующей формуле:

V=n*(R₁²+R₂²+R₁*R₂)*H/3.

Конус и его сечение плоскостью

Перу древнегреческого математика Аполлония Пергского принадлежит теоретический труд «Конические сечения». Благодаря его работам в геометрии появились определения кривых: параболы, эллипса, гиперболы. Рассмотрим, причем здесь конус.

Возьмем прямой круговой конус. Если плоскость пересекает его перпендикулярно оси, то в разрезе образуется круг. Когда секущая пересекает конус под углом к оси, то в разрезе получается эллипс.

Секущая плоскость, перпендикулярная основанию и параллельная оси конуса, образует на поверхности гиперболу. Плоскость, разрезающая конус под углом к основанию и параллельная касательной к конусу, создает на поверхности кривую, которую назвали параболой.

Решение задачи

Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.

Дано:

V=10 л=10 дм³;

R₁=15 см;

R₂=25 см.

Развертка конуса имеет вид, схематически приведенный на рисунке 3.

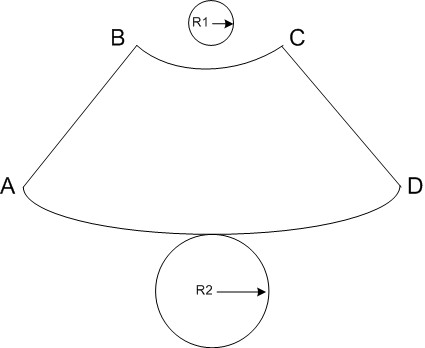
L - образующая конуса.

Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:

S=n*(R₁+R₂)*L,

необходимо вычислить образующую. Ее находим из величины объема V=n*(R₁²+R₂²+R₁*R₂)*H/3.

Отсюда H=3V/n*(R₁²+R₂²+R₁*R₂).

Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.

L²=(R_2-R₁)²+H².

Теперь у нас имеются все данные, чтобы построить чертеж ведра.

Почему пожарные ведра имеют форму конуса?

Кто задумывался, почему пожарные ведра имеют, казалось бы, странную коническую форму? А это не просто так. Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.

Во-первых, как оказывается, пожарное ведро быстрее наполняется водой и при переноске она не расплескивается. Конус, объем которого больше обычного ведра, за один раз позволяет перенести больше воды.

Во-вторых, воду из него можно выплеснуть на большее расстояние, чем из обычного ведра.

В-третьих, если коническое ведро сорвется с рук и упадет в огонь, то вся вода выливается на очаг возгорания.

Все перечисленные факторы позволяют сэкономить время — главный фактор при тушении пожара.

Практическое применение

У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.

А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.

Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда. Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.

Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.

Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:

• воронки-лейки для наливания жидкостей;
• рупор-громкоговоритель;
• парковочные конусы;
• абажур для торшера;
• привычная новогодняя елочка;
• духовые музыкальные инструменты.

Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.