Как рассчитать объем различных геометрических тел?
В курсе стереометрии один из главных вопросов - как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
В жизни тоже часто приходится сталкиваться с подобными задачами. Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Свойства, справедливые для объема каждого тела
- Это значение - всегда положительное число.
- Если тело удается разделить на части так, чтобы не было пересечений, то общий объем оказывается равным сумме объемов частей.
- У равных тел одинаковые объемы.
- Если меньшее тело полностью помещается в большем, то объем первого меньше, чем второго.
Общие обозначения для всех тел
В каждом из них есть ребра и основания, в них строятся высоты. Поэтому такие элементы для них одинаково обозначены. Именно так они записаны в формулах. Как рассчитать объем каждого из тел - узнаем дальше и применим на практике новые умения.
| Обозначение | Пояснение |
| а | ребро тела, у которого они все равны |
| V | объем |
| S0 | площадь основания |
| h | высота |
| r | радиус |
В некоторых формулах имеются другие величины. Об их обозначении будет сказано при появлении такой необходимости.
Призма, параллелепипед (прямой и наклонный) и куб
Эти тела объединены, потому что внешне очень похожи, и формулы того, как рассчитать объем, идентичны:
V = S0 * h.
Различаться будет только S0. В случае с параллелепипедом она рассчитывается, как для прямоугольника или квадрата. В призме основанием может оказаться треугольник, параллелограмм, произвольный четырехугольник или другой многоугольник.
Для куба формула существенно упрощается, потому что все его измерения равны:
V = а3.
Пирамида, тетраэдр, усеченная пирамида
Для первого из указанных тел существует такая формула, чтобы вычислить объем:
V = 1/3 * S0 * н.
Тетраэдр является частным случаем треугольной пирамиды. В нем все ребра равны. Поэтому снова получается упрощенная формула:
V = (а3 * √2) / 12, или V = 1/3 S0 h
Усеченной пирамида становится тогда, когда у нее срезана верхняя часть. Поэтому ее объем равен разности двух пирамид: той, которая была бы целой, и удаленной верхушки. Если есть возможность узнать оба основания такой пирамиды (S1 — большее и S2 — меньшее), то удобно пользоваться такой формулой для расчета объема:
V = 1/3 * h * (S1 + √(S1S2) + S2).
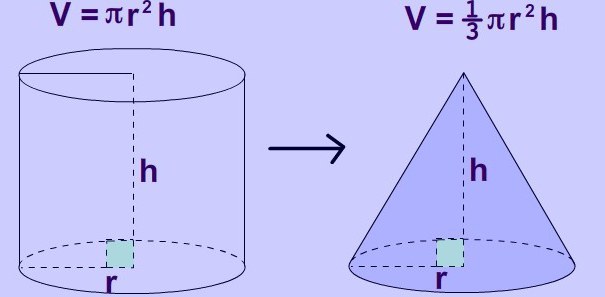
Цилиндр, конус и усеченный конус
Если требуется рассчитать объем цилиндра, можно воспользоваться формулой, которая указана для призмы. Иногда удобно записать ее в таком виде:
V =π * r2 * h.
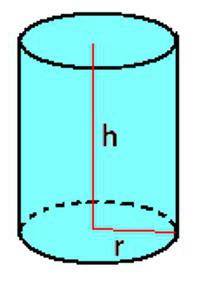
Несколько сложнее обстоит дело с конусом. Для него существует формула:
V = 1/3 π * r2 * h. Она очень похожа на ту, что указана для цилиндра, только значение уменьшено в три раза.
Так же, как с усеченной пирамидой, дело обстоит непросто с конусом, который имеет два основания. Формула для вычисления объема усеченного конуса выглядит так:
V = 1/3 π * h * (r12 + r1r2 + r22). Здесь r1 — радиус нижнего основания, r2 — верхнего (меньшего).
Шар, шаровые сегменты и сектор
Это самые сложные для запоминания формулы. Для объема шара она выглядит так:
V = 4/3 π *r3.
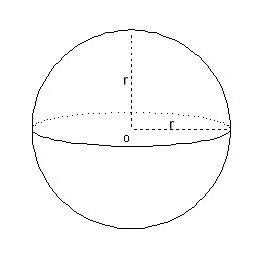
В задачах часто есть вопрос о том, как рассчитать объем шарового сегмента — части сферы, которая как бы срезана параллельно диаметру. В этом случае на выручку придет такая формула:
V = π h2 * (r - h/3). В ней за h взята высота сегмента, то есть та часть, которая идет по радиусу шара.
Сектор делится на две части: конус и шаровой сегмент. Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
V = 2/3 πr2 * h. Здесь h также высота сегмента.
Примеры задач
Про объемы цилиндра, шара и конуса
Условие: диаметр цилиндра (1 тело) равен его высоте, диаметру шара (2 тело) и высоте конуса (3 тело); проверить пропорциональность объемов V1 : V2 : V3 = 3:2:1
Решение. Сначала потребуется записать три формулы для объемов. Потом учесть, что радиус — это половина диаметра. То есть высота будет равна двум радиусам: h = 2r. Произведя простую замену получается, что формулы для объемов будут иметь такой вид:
V1 = 2 π r3; V3 = 2/3 π r3. Формула для объема шара не изменяется, потому что в ней не фигурирует высота.
Теперь осталось записать отношения объемов и произвести сокращение 2π и r3. Получается, что V1 : V2 : V3 = 1 : 2/3 : 1/3. Эти числа легко привести к записи 3 : 2 : 1.
Ответ. V1 : V2 : V3 = 3 : 2 : 1.
Про объем шара
Условие: имеется два арбуза радиусами 15 и 20 см; как их выгоднее съесть: первый вчетвером или второй ввосьмером?
Решение. Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго - восьмая.
Осталось записать отношение объемов частей. Оно будет выглядеть так:
(V1 : 4) / (V2 : 8) = (1/3 π r13) / (1/6 π r23). После преобразования остается только дробь: (2 r13) / r23. После подстановки значений и вычисления получается дробь 6750/8000. Из нее ясно, что часть от первого арбуза будет меньше, чем от второго.
Ответ. Выгоднее съесть восьмую часть от арбуза с радиусом 20 см.
Про объемы пирамиды и куба
Условие: имеется пирамида из глины с прямоугольным основанием 8Х9 см и высотой 9 см; из этого же куска глины сделали куб; чему равно его ребро?
Решение. Если обозначить стороны прямоугольника буквами в и с, то площадь основания пирамиды вычисляется, как их произведение. Тогда формула для ее объема:
V1= 1/3 * вс * h.
Формула для объема куба написана в статье выше. Эти два значения равны: V1 = V2. Осталось приравнять правые части формул и сделать необходимые вычисления. Получается, что ребро куба будет равно 6 см.
Ответ. а = 6 см.
Про объем параллелепипеда
Условие: требуется сделать ящик вместимостью 0,96 м3, известны его ширина и длина - 1,2 и 0,8 метра; какой должна быть его высота?
Решение. Поскольку основание параллелепипеда - прямоугольник, его площадь определяется как произведение длины (а) на ширину (в). Поэтому формула для объема выглядит так:
V = а * в * н.
Из нее легко определить высоту, разделив объем на площадь. Получится, что высота должна быть равна 1 м.
Ответ. Высота ящика равна одному метру.
Похожие статьи
- Как рассчитать объем груза и зачем это делать
- Объем конуса, его расчет
- Как рассчитать квадратные метры наиболее просто
- Фундамент под гараж: расчет, строительство, стоимость
- Сколько бруса в кубе 100х100: пример расчета. Размер бруса
- Цилиндр. Виды, объём цилиндра, площадь поверхности
- Как высчитать проценты правильно
