Мощность тока в электрических цепях

Одним из параметров, характеризующих поведение электронов в электрической цепи, кроме напряжения и тока, выступает мощность. Она является мерой количества работы, которую можно совершить за единицу времени. Работу обычно сравнивают с подъёмом веса. Чем больше вес и высота его подъёма, тем больше работы выполнено. Мощность определяет быстроту совершения единицы работы.

Единицы измерения

Мощность автомобилей исчисляют в лошадиных силах – единице измерения, придуманной изготовителями паровых двигателей с целью измерения работоспособности своих агрегатов в обычном источнике энергии того времени. Мощность автомобиля не говорит, как высоко он может заехать на холм или сколько веса он может перевезти, а только показывает, как быстро он это сделает.

Мощность двигателя зависит от его скорости и вращающего момента выходного вала. Скорость измеряют в оборотах в минуту. Вращающий момент – это момент силы двигателя, который измерялся первоначально в фунт-футах, а сейчас в ньютон-метрах или джоулях.

Тракторный двигатель в 100 л. с. вращается медленно, но с большим крутящим моментом. Мотоциклетный двигатель равной мощности вращается быстро, но с небольшим крутящим моментом. Уравнение расчёта мощности имеет вид:

P = 2π S T / 33000, где S – скорость вращения, об/мин, а T – момент вращения.

Переменными здесь являются момент и скорость. Иначе говоря, мощность прямо пропорциональна ST: P~ST.

Мощность постоянного тока

В электроцепях мощность находится в функциональной зависимости от напряжения и тока. Неудивительно, что она похожа на вышеприведённое уравнение P=IU.

Но тут P не пропорциональна току, умноженному на напряжение, а равняется ему. Исчисляется в ваттах, сокращённо Вт.

Важно знать, что ток и напряжение отдельно мощность не определяют, лишь их совокупность. Напряжение является работой на единицу электрического заряда, а ток – скоростью движения зарядов. Напряжение (эквивалент работы) подобно работе при подъёме веса в противодействие силе гравитации. Ток (эквивалентен скорости) подобен скорости подъёма веса. Их произведение и составляет мощность.

Как тракторный и мотоциклетный моторы, цепь с высоким напряжением и небольшим током способна быть одинаковой мощности с цепью невысокого напряжения и большим током. Напряжение и ток вне взаимосвязи не могут характеризовать мощность электроцепи.

Разомкнутая цепь с напряжением и нулевой силой тока работы не совершает, вне зависимости от высоты напряжения. Ведь, согласно формуле, что угодно, умноженное на 0, даёт 0: P = 0 U = 0. В замкнутой цепи из сверхпроводящего провода с нулевым сопротивлением можно достичь тока при напряжении, равном нулю, что также не приведёт к рассеиванию энергии: P = I 0 = 0.

Лошадиные силы и ватты обозначают одно и то же: количество работы, которую можно совершить за единицу времени. Эти единицы взаимосвязаны соотношением

1 л. с. = 745,7 Вт

Пример расчёта

Итак, мощность тока электроцепи в ваттах равняется произведению напряжения на ток.

Чтобы определить, например, мощность нагрузки сопротивлением 3 Ом, в цепи с батареей питания напряжением 12 В, необходимо, применив закон Ома, найти ток

I = U/R = 12/3 =4 А

Умножение полученной силы тока на напряжение и даст искомый результат:

P = I U = 4 А 12 В = 48 Вт

Таким образом, лампа потребляет 48 Вт.

Что же произойдёт при увеличении напряжения?

При напряжении 24 В и сопротивлении 3 Ом ток

I= U/R = 24/3 =8 А

При удвоении напряжения удвоилась и сила тока.

P = IU = 8 А 24 В = 192 Вт

Мощность также увеличилась, но больше. Почему? Потому что это функция произведения напряжения на ток, напряжение и ток увеличились в 2 раза, следовательно, мощность возросла в 4 раза. Это можно проверить делением 192 ватт на 48, частное от которого равно 4.

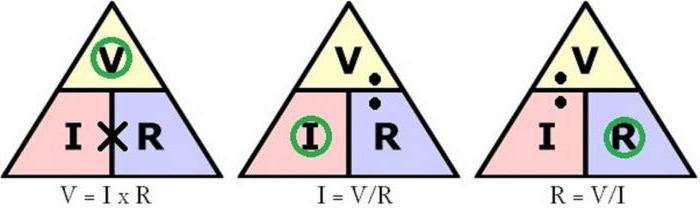
Варианты формулы

Применив алгебру для преобразования формулы, можно взять исходное уравнение и преобразовать его для случаев, когда неизвестен один из параметров.

Если даны напряжение и сопротивление:

P = (U/R) U или P = U²/R

При известной силе тока и сопротивлении:

P = I (I R) или P = I² R

Исторический факт: отношение между рассеиваемой мощностью и силой тока через сопротивление открыл Джеймс Прескотт Джоуль, а не Георг Симон Ом. Оно было опубликовано в 1841 г. в виде уравнения P = I² R и носит название закона Джоуля–Ленца.

Уравнения мощности:

• P = U I
• P = I² R
• P = U²/R

Переменный ток

Закон Ома и Джоуля–Ленца были установлены для постоянного тока, но они справедливы и для мгновенных значений изменяющегося тока и напряжения.

Мгновенное значение P равно произведению мгновенных значений силы тока и напряжения с учётом их смещения по фазе на угол φ:

P(t) = U(t)I(t) = U_m cosωt I_m cos(ωt-φ) = (1/2)U_m I_m cosφ + (1/2) U_m I_m cos(2ωt-φ).

Из уравнения следует, что у мгновенной мощности есть постоянная составляющая, и она совершает колебательные движения вокруг среднего значения с частотой, которая вдвое превышает частоту тока.

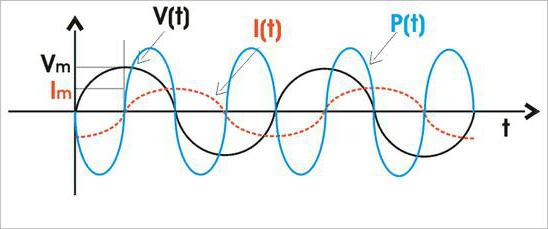
Среднее значение P(t), представляющее практический интерес, равно:

P = (U_m I_m /2) cosφ

С учётом того, что cos φ=R/Z, где Z=(R² + (ωL - 1/ω C)²)^1/2 и U_m/Z = I_m,

P = (R I_m²)/2

Здесь I = I_m 2^-1/2 = 0,707 I_m – эффективное значение силы тока, А.

Аналогично U = U_m 2^-1/2 = 0,707 U_m – эффективное напряжение, В.

Средняя мощность через эффективное напряжение и ток определяется

P = U I cos φ, где cos φ – коэффициент мощности.

P в электроцепи переходит в тепловую или другой вид энергии. Наибольшей активной мощности можно достичь при cosφ=1, то есть при отсутствии сдвига фаз. Она носит название полной мощности

S = U I = Z I² = U²/Z

Её размерность совпадает с размерностью P, но с целью отличия S измеряется вольт-амперами, ВА.

Степень интенсивности обмена энергией в электроцепи характеризуется реактивной мощностью

Q = U I sinφ = U I_p = U_p I = X I² = U²/X

Она имеет размерность активной и полной, но с целью различения её выражают вольт-амперами реактивными, ВАр.

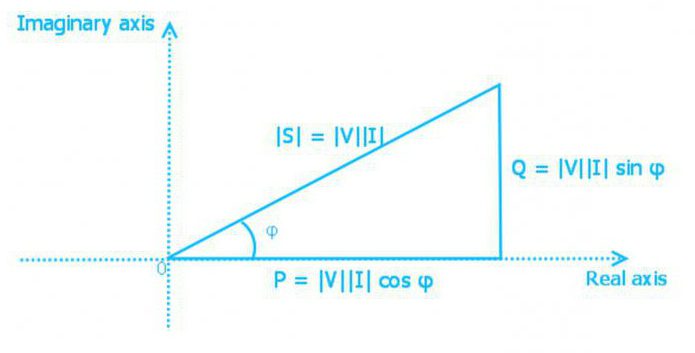
Треугольник мощностей

Мощность активная, реактивная и полная взаимосвязаны выражением

S = (P ²+ Q²)^1/2

Мощность представляют в виде стороны прямоугольного треугольника. Используя законы тригонометрии, можно найти длину одной стороны (количество мощности любого типа) по двум известным сторонам или по длине одной и углу. В таком треугольнике активная мощность является прилежащим катетом, реактивная – противолежащим, а полная мощность – гипотенузой. Угол между катетом активной мощности и гипотенузой равен углу фазы импеданса Z электрической цепи.

Комплексная форма записи этой взаимосвязи следующая:

S = P+jQ = U I cosφ + j U I sinφ= U I e^jφ = U I*, где

S – комплексная мощность;

I* – комплексное сопряжённое значение тока.

Вещественная составляющая комплекса – активная, а мнимая – реактивная.

Мгновенная полная мощность всегда остаётся постоянной величиной.

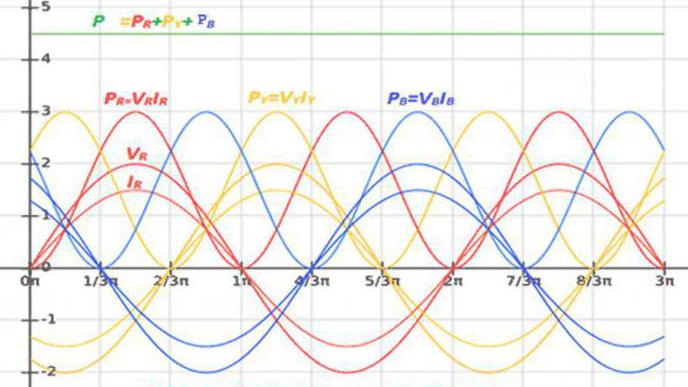
Мощность трёхфазного тока

Нагрузка каждой фазы трёхфазной электроцепи преобразует энергию или обменивается ею с источником питания. Вследствие этого P и Q цепи равняются суммарной мощности всех фаз:

P = P_r + P_y + P_b; Q = Q_r + Q_y + Q_b – соединение «звезда»;

P = P_ry + P_yb + P_br; Q = Q_ry + Q_yb + Q_br – соединение «треугольник».

Активные и реактивные мощности каждой фазы определяются, как в однофазной цепи.

Полная мощность трёхфазной цепи:

S = (P²+Q²)^1/2,

что в комплексной форме имеет вид

S = P+jQ = (P_r + P_y + P_b) + j(Q_r + Q_y + Q_b )= S_r + S_y + S_b= U_r I_r + U_y I_y + U_b I_b

Симметричная нагрузка фаз имеет следствием равенство их мощностей. Вот почему мощность тока равна утроенной активной и реактивной мощности фазы:

P = 3P_ф = 3 I_ф U_ф cosφ_ф = 3 R_ф I_ф²

Q = 3 Q_ф = 3 I_ф U_ф sinφ_ф = 3 X_ф I_ф²

S = 3 S_ф = 3 I_ф U_ф

I_ф и U_ф здесь можно заменить их линейными значениями, учитывая, что для звезды U_ф=U_л; I_ф=I_л, а для треугольника U_ф=U_л; I_ф=I_л3^-1/2:

P = 3^1/2 I_л U_л cosφ_ф;

Q = 3^{1/2 I_л U_л} sinφ_ф;

S = 3^{1/2 I_л U_л}.

Ток несинусоидальной формы

Определение P в цепи несинусоидального тока аналогично её определению в цепи тока синусоидального, так как за период T средняя мгновенная мощность

P = 1/T∫u i dt

Активная мощность тока определяется суммой P гармонических составляющих, в том числе и постоянной, являющейся гармоникой нулевой частоты.

Реактивная мощность тока подобным образом является результатом сложения Q каждой гармоники.

Q = ∑U_k I_k sinφ_k = ∑ Q_k

Полная мощность определяется произведением эффективного тока и напряжения:

S = I U.