Теория графов: основные определения

Теория графов – раздел математики, используемый в информатике и программировании, экономике, логистике, химии.

Что такое граф

Часто для описания строения систем используют графические схемы. Элементы в них изображают кружками, точками, квадратами и т. п., а связи между элементами – линиями или стрелками. При этом ни то, как изображаются элементы, ни длина или форма линий не важны – имеет значение только, какие элементы соединены. Итак, граф – это пара вида (A, M), где A – конечное множество вершин, а M – множество ребер – линий, связывающих некоторые вершины.

Основные понятия теории графов

У ориентированного графа или орграфа (см. рисунок ниже) ребра ориентированы, называются дугами и изображаются стрелками. Дуга может быть обозначена упорядоченной парой вершин, которые она связывает, – начальной и конечной.

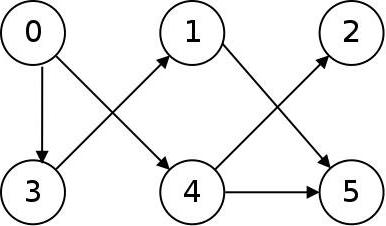
У неориентированного графа (см. рисунок ниже) ребра изображаются линиями без ориентации. Соответственно, пара вершин, которую связывает ребро, является неупорядоченной. Обе эти вершины есть концы ребра.

Если вершины a и b – концы ребра (или начало и конец дуги) графа, то говорят, что вершины a и b инцидентны этому ребру (дуге), также ребро (дуга) инцидентно вершинам a и b. Если вершины a и b – концы ребра, то они (a и b) называются смежными.

Чаще всего рассматривают графы, ребра которых имеют один тип – являются ориентированными или нет.

Если ребра имеет одинаковые начало и конец, то их называют кратными ребрами, а граф, в котором они присутствуют, называется мультиграфом.

Теория графов также использует понятие «петля» – ребро, выходящее и заходящее в одну и ту же вершину. Граф, в котором есть петли, называется псевдографом.

Чаще всего встречаются неориентированные графы, у которых нет кратных ребер и нет петель. Такие графы называются обыкновенными. Они не имеют кратных ребер, поэтому можно отождествить ребро и соответствующую пару вершин.

Каждая вершина орграфа характеризуется:

• Полустепенью исхода. Это количество дуг, выходящих из нее.
• Полустепенью захода. Это количество дуг, которые входят в данную вершину.

Сумма полустепеней захода орграфа, а также сумма полустепеней исхода равны общему количеству дуг графа.

У неориентированного графа каждая вершина характеризуется степенью вершины. Так называется количество ребер, которые инцидентны вершине. Общая сумма степеней вершин графа есть количество ребер, умноженное на два: каждое ребро будет давать вклад, который равен двум.

Вершина со степенью 0 называется изолированной.

Висячей вершиной является вершина со степенью 1.

Теория графов называет пустым графом такой, в котором нет ни одного ребра. Полный граф – это обыкновенный граф, в котором смежны любые 2 вершины.

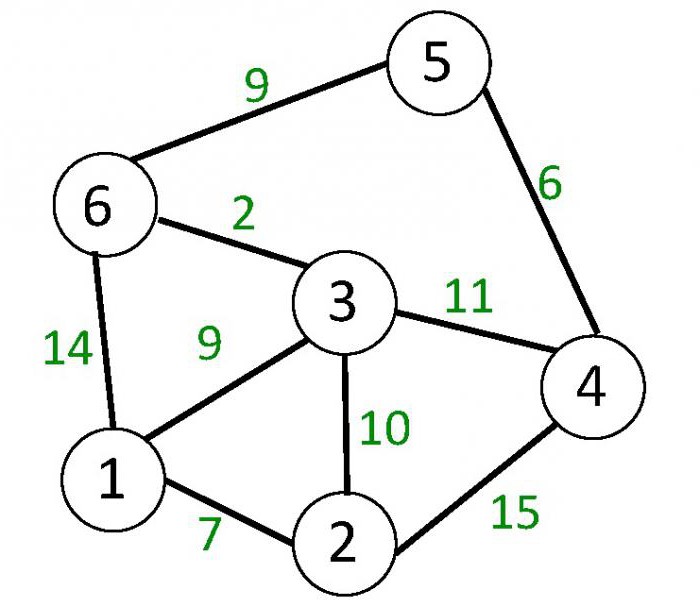
Взвешенные графы – это графы, вершинам или ребрам (дугам) которых или и вершинам, и ребрам (дугам) сразу, приписываются некоторые числа. Они называются весами. На втором рисунке показан неориентированный граф, ребра которого взвешены.

Графы: изоморфизм

Понятие изоморфизма используется в математике. В частности, теория графов определяет его так: два графа U и V изоморфны, если в этих графах существует биекция между множествами их вершин: каждые 2 вершины в графе U соединены ребром в том и только том случае, если в графе V связаны ребром те же вершины (которые могут по-другому называться). На рисунке ниже показаны два изоморфных графа, в которых между вершинами, окрашенными в одинаковые цвета и в первом, и во втором графе, существует вышеописанная биекция.

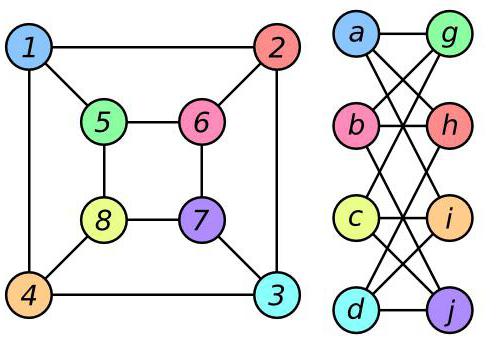
Пути и циклы

Путем в неориентированном или ориентированном графе является последовательность ребер, где каждое следующее начинается в вершине, в которой заканчивается предыдущее. Простой путь – такой, в котором все вершины, исключая, может быть, начальную и конечную, и ребра различны. Циклом в орграфе называется путь, у которого совпадают начальная и конечная вершины и который включает не менее одного ребра. Циклом в неориентированном графе является путь, который содержит не менее трех различных ребер. На втором рисунке циклом является, например, путь (3, 1), (6, 3), (1, 6).

Теория графов в программировании используется для построения граф-схем алгоритмов.