Пример алгоритма Диффи Хеллмана

Раскрытие темы криптографии об открытых ключах необходимо начать с исторического пути возникновения данной задачи. Whitfield Diffie и Martin Hellman были первыми, кто задался вопросом об открытом способе передаче ключей. Произошло это в 1976 году. В публикации были сделаны первые попытки разобраться с возникшей проблемой. Их решение не было лишено недостатков, однако положило начало совершенно иному способу мышления в области шифрованной передачи данных.

Предпосылки создания алгоритма Диффи-Хеллмана

Аутентификация и шифрование до этого момента были возможны лишь посредством общего секретного ключа. С развитием технологий вопрос становился более острым. Если 10 людям необходим передавать данные между собой по небезопасным каналам, им потребуется обмениваться паролями друг с другом. Данная задача выглядит вполне реальной. Даже с учетом необходимости их обновления. Ведь для 10 друзей понадобится всего 45 секретных ключей. А если контактов будет 100? Понадобится 4950 паролей. Ситуация нарастает как снежный ком.

Главным достижением Диффи и Хеллмана стала правильная постановка вопроса и остроумный ответ на него. Они предположили, что данные можно шифровать одним способом, а расшифровывать - другим. То есть иметь 2 ключа. Тот, что используется для шифрования, можно оставить открытым. Таким образом любой человек сможет зашифровать сообщение, но расшифровать смогут его только обладатели второго секретного ключа. Но как реализовать алгоритм передачи такого ключа? Ученые смогли частично и на это дать ответ.

Краткая математика: группы

Алгоритм или протокол Диффи-Хеллмана (далее DH) работает при помощи простых чисел. Пусть а - это достаточно большое число, принадлежащее множеству простых чисел. Алгоритм предполагает использование числа размером 250-500 байт. Пусть Z_а - мультипликативная группа кольца вычетов по модулю а, которая будет использована алгоритмом шифрования Диффи-Хеллмана. Она состоит из множества чисел 1, ..., a-1.

Возьмем некий элемент b из группы Z_а и рассмотрим бесконечную последовательность 1, b, b², b³, b⁴, ... Из того факта, что группа Z_a по определению является конечным множеством, рано или поздно рассматриваемая последовательность {b} начнет повторяться. Положим bⁱ = b^j (i < j).

Теперь разделим каждую часть равенства на bⁱ (по модулю a) и получим b^j-i = 1. Это значит, что существует такое число k = j-i, для которого верно b^k = 1 (mod a). Самое маленькое число k, для которого выполняется данное равенство, называется порядком числа b. Во избежание недопонимания с другой специальной литературой для объяснения системы Диффи-Хеллмана используются стандартные математические обозначения.

Таким образом, возводя число b, называемое образующим элементом, в степень, мы получаем последовательность чисел (множество) 1, ..., b^k-1 . Количество элементов данного множества в точности равно k.

Свойство умножения по модулю a гласит, что существует хотя бы одно число b, порождающее все элементы группы Z*_a . Иначе говоря существует число для которого верно k = a - 1. Данное свойство позволяет представить числа группы Z*_a в виде 1, b, b², ... b^a-2 . Такое число b называется примитивным числом группы.

В дальнейшем по признакам группы легко доказывается, что множество, порожденное числом b, также само является группой и наследует все свойства групп. Иными словами, операции внутри порожденной группы или подгруппе можно проводить точно таким же образом, как в группе по модулю a.

Рассмотрим утверждение. Для любого элемента b его порядок является делителем числа a-1. Это легко показать. Пусть a=7. Число b = 3 - примитивное, т. к. 1, ..., b⁵ = 1, 3, 2, 6, 4, 5. Тогда число h = 2 будет порождать подгруппу 1, ..., h² = 1, 2, 4, так как h³ = 2³ mod 7 = 1. h = 6 порождает подгруппу 1, 6. Размеры групп равны 3 и 2, соответственно. Очевидно, что они являются делителями числа a-1 = 6.

Первый алгоритм DH

В первоначальной версии алгоритм работал по следующей схеме. Выбираются большое число a из множества простых и примитивный элемент b, порождающий Z*_a. Оба числа a и b представляют собой открытый ключ, они известным всем, в том числе и злоумышленникам. Как же тогда скрыть сообщения?

Именно на этом шаге Диффи и Хеллман придумали очень остроумный ход. Пусть у нас есть два человека, связывающихся между собой: А и Б. Сначала А выбирает случайное число x из Z*_a , что является эквивалентом выбора числа из {1, ..., a-1}. Затем он вычисляет значение по формуле (b^x mod a) и отправляет его Б. В свою очередь Б выбирает некоторое число y из того же множества, вычисляет значение (b^y mod a) и отправляет результат обратно А.

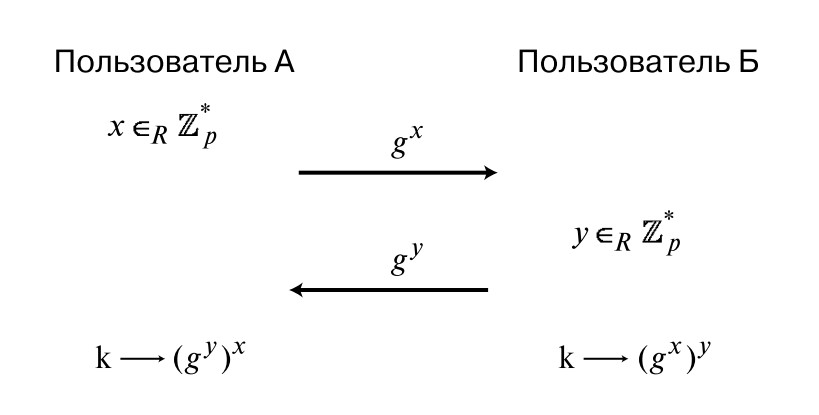
Таким хитрым способом получается, что секретный ключ выглядит b^xy . Благодаря свойству степеней, которое гласит g^xy = (g^y)^x, собеседник А может вычислить нужное значение и расшифровать пересланную ему информацию. И точно так же это значение вычисляет собеседник Б. Таким образом, оба имеют одинаковый секретный ключ.

Какие проблемы испытывает злоумышленник при таком обмене информацией? Он может перехватить числа g^x и g^y. И даже при знании открытых ключей задача вычисления g^xy не является тривиальной, т. к. пока не существует эффективного алгоритма поиска нужного значения в распределении ключей Диффи-Хеллмана. Данная задача известна под названием "проблема вычисления дискретного логарифма".

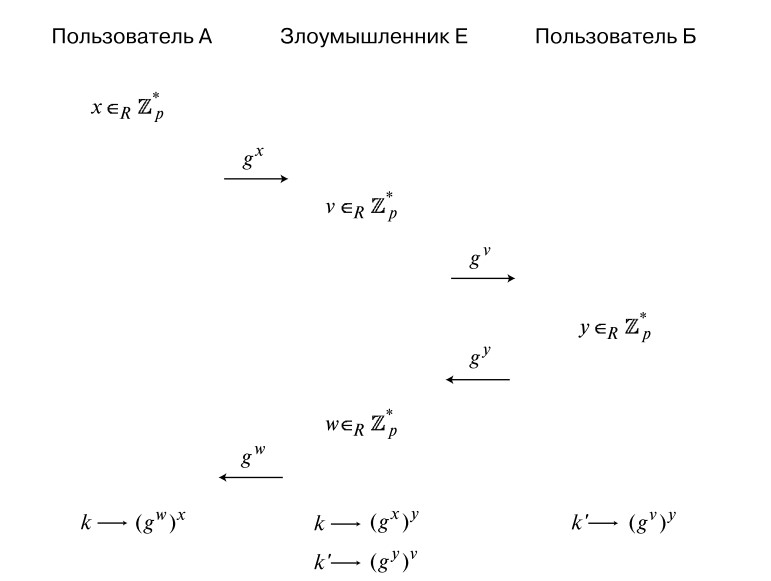
Атака посредника

Одной из слабостей первичного алгоритма Диффи-Хеллмана является его незащищенность против атак посредника. Что это значит? Собеседник А знает, что он общается с неким лицом, но конкретно с кем - он понятия не имеет. Таким образом, злоумышленник может вклиниться в передачу информации и имитировать собеседника Б при общении с А, и наоборот. Ни один из них не сможет заподозрить неладное.

Существует лишь одна область применения, при которой атаки на алгоритм Диффи-Хеллмана исключены. Это телефон и видеосвязь. Здесь собеседники способны узнать друг друга, поэтому посредник не сможет вклиниться.

Подводные камни

Помимо атаки посредника протокол DH таит в себе массу других проблем. Например, одним из недостатков является случай, когда в роли образующего числа a выступает не примитив. Тогда он порождает лишь подгруппу. Из-за сужения количество возможных вариантов злоумышленнику открывается возможность их перебора.

Проблем из-за этого недочета можно избежать, если каждый из собеседников перед началом обмена данными будет проверять, что числа a и b выбраны правильно. То есть a является простым числом, а b - примитивом. Однако когда дело доходит до соблюдения безопасности посредством выполнения определенных однообразных необязательных шагов, пользователи часто их игнорируют.

Другая серьезная проблема возникает на основе подгрупп по модулю a. Если злоумышленник решит поменять g^x на 1, чтобы облегчить себе процесс подслушивания, то пользователи смогут легко его обнаружить, проверив число на соответствие. Однако, если он подменит ключ числом с низким порядком, пользователи не смогут ничего заподозрить. А так как количество элементов в множестве с низким порядком будет невелико, то злоумышленнику для расшифровки нужно будет перебирать небольшое количество вариантов.

Надежность простых чисел

В алгоритме DH используется большое и надежное число из множества простых. Как именно его выбрать? Разберем по шагам.

1. Подобрать по формуле a = 2k+1 числа a и k такие, чтобы они были простыми.
2. Из множества 1, ..., a-1 исключить 1 и a-1.
3. Взять случайное число x из оставшегося после второго шага множества и найти значение b = x²(мод a).
4. Убедиться, что b не равно 1 или a-1. Если b окажется равным одному из запрещенных значений, следует выбрать другое x. И повторить операции.

Полученный таким образом набор (a, k, b) может считаться достаточным для использования в алгоритме обмена ключами Диффи-Хеллмана. Соответственно, получателю сообщения также требуется проверить значение, которое должно являться степенью b, и убедиться (например, функцией символа Лежандра), что оно попадает в множество, порожденное числом b.

Использование подгрупп

Главным минусом вышеописанного алгоритма является недостаточная эффективность. Допустим, что длина простого числа a составляет n бит, значит, k - n-1 бит. Получается, все степени будут иметь длину n-1. Тогда операция возведения в степень в среднем будет состоять из 3n/2 умножений по mod a. Это достаточно большой процесс.

Для того чтобы справиться с этой проблемой, было решено применять подгруппы меньшего размера. Каков выигрыш в производительности в таком случае? Если число a состоит из 2000 бит, тогда для вычисления b^x требуется 3000 операций умножения. Благодаря использованию подгрупп, это число может быть сокращено до ~400. Это существенное увеличение эффективности алгоритма делает возможным его всестороннее применение. Например, алгоритм Диффи-Хеллмана с тремя и более участниками.

Какой должна быть длина числа a

Правильный подбор размеров параметров алгоритма Диффи-Хеллмана — задача достаточно сложная. Обычным требованием в мире криптографии является, например, условие, чтобы для взлома системы злоумышленнику понадобилось не менее 2¹²⁸ шагов. Если в алгоритмах симметричного шифрования соблюдать подобное требование достаточно легко, то в алгоритмах с открытым ключом это представляется реальной проблемой. Если соблюдать вышеназванное требование, то длина a должна состоять по меньшей мере из 850 байт.

На практике такой размер создает большие проблемы производительности в системе, т. к. операции с открытым ключом выполняются гораздо дольше, нежели, например, в симметричных шифрованиях с ключами 128 или 256 бит. Тогда как быть? Минимальная длина открытого ключа должна начинаться от 2048 бит. Хотя чем длиннее ключ, тем выше уровень безопасности. Следует рассматривать в первую очередь возможности производительности системы и ее стоимость. Если она позволяет использовать ключ размерами 4096 бит, нужно это делать.

Как производится оценка требуемого уровня безопасности

Размеры ключей в симметричных шифрованиях остаются неизменными (128, 256 бит) всю жизнь системы, тогда как размеры открытого ключа всегда представляют собой переменную величину. Если предстоит разработать систему, которая должна использоваться 30 лет и хранить данные в секрете не менее 20 лет после вывода системы из использования, то размер ключа симметричного шифрования изначально должен быть достаточно большим, чтобы защищать систему следующие 50 лет.

Из-за очевидных проблем производительности, из-за того что в алгоритме Диффи-Хеллмана шифрование происходит значительно большим числом операций, требования к открытым ключам отличаются. Он остается действительным на протяжении одного года и защищает данные следующие 20 лет, то есть в общей сложности используется 21 год. Ввиду его переменного размера ключ каждый год может изменяться и создаваться все более длинным, чтобы обеспечить требуемый уровень безопасности.

Так, например, лучшие оценки показывают, что ключ длиной 256 байт способен обеспечить защиту данных на ~20 лет, длиной 384 байт - 35 лет, а при длине 512 байт - 47 лет и т. д. Число 6800 бит, гарантирующее, что злоумышленнику потребуется 2¹²⁸ шагов для его взлома, получено из подобных оценок. Однако это всего лишь прогноз, доверять которому нужно с большой осторожностью. Можно достаточно точно предсказать развитие событий на 10 лет вперед, но на 50 - это фантастика.

Практические рекомендации

Приведем несколько практических советов относительно использования протокола DH. Выбирать в качестве k следует простое число размером 256 бит. Это минимум, который способен обеспечить хоть сколько-то адекватный уровень безопасности против атак. В качестве a выбрать число, которое имело бы вид Na+1, где N - некоторое целое число. О размерах числа a было сказано ранее. После этого выбирается случайное число b и проверяется на несколько условий. Во-первых, оно не может быть единицей. Во-вторых, b^k = 1.

В свою очередь, любой участник общения должен убедиться в следующем:

• a и k - простые числа, длина k составляет 256 бит, длина p достаточно велика.
• число k является делителем a-1.
• b не равно 1 и b^k = 1.

Данные условия следует проверять даже при безоговорочном доверии к источнику.

Заключение

Алгоритм DH является остроумным решением одной из серьезных проблем и по сей день активно используется в модифицированном под современные требования безопасности виде в различных протоколах. Алгоритм Диффи-Хеллмана, к примеру, используется в некоторых частях реализации протокола IKE. Однако его применение должно быть методичным и аккуратным ввиду наличия очевидных проблем и серьезных подводных камней.