Геометрическая фигура призма: определение, виды, формулы площади поверхности и объема

Автор Валерий Савельев January 3, 2019

Стереометрия - важный раздел геометрии, изучающий свойства фигур в трехмерном пространстве. В данной статье с точки зрения стереометрии рассмотрим класс геометрических объектов, который называется призмы, дадим определение призмы и перечислим ее основные виды и характеристики.

Что такое призма?

Прежде чем дать определение призмы, представим себе произвольный многоугольник на плоскости. Воспользовавшись операцией параллельного переноса этого многоугольника в пространстве, мы получим объемную фигуру. Эта фигура будет состоять из двух одинаковых многоугольников и нескольких параллелограммов. Это и есть призма произвольной формы. Рисунок ниже показывает, как выглядит шестиугольная призма.

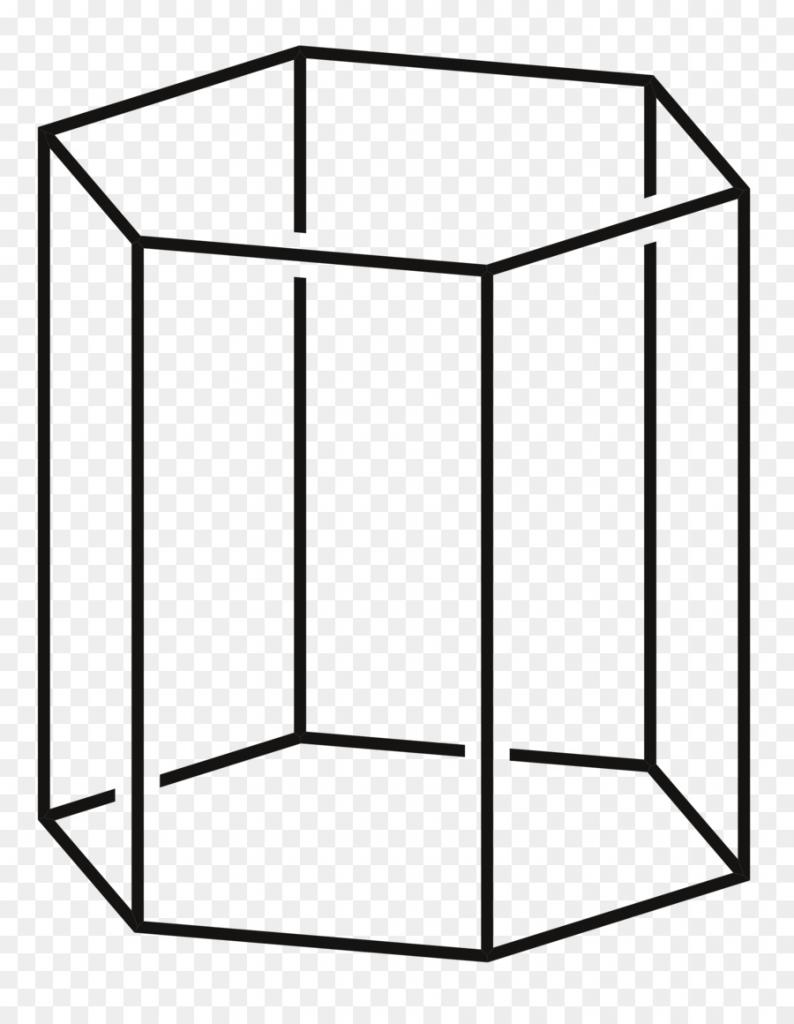
Таким образом, можно дать следующее определение призмы: это объемная фигура, которая образована n параллелограммами и двумя одинаковыми n-угольными сторонами, расположенными в параллельных плоскостях. Одинаковые n-угольники называются основаниями фигуры, а ее параллелограммы образуют боковую поверхность.

Элементы призмы и ее параметры

В соответствии с определением призмы, можно выделить ее грани, вершины и ребра. Количество граней фигуры равно n+2, из которых 2 грани являются многоугольными основаниями. Количество вершин равно 2*n. Все они являются равноправными и образованы пересечением основания и двух боковых параллелограммов. Наконец, число ребер любой призмы составляет 3*n, причем 2*n ребер относятся к основаниям, а n ребер являются боковыми (образованы пересечением параллелограммов).

Призма - это совершенный многогранник, числа ребер, вершин и граней которого связаны следующим равенством:

число ребер = число граней + число вершин - 2.

Латинская буква n - это количество сторон (вершин) плоского многоугольника в основании.

Линейными параметрами призмы, знание которых позволяет однозначно определить ее геометрические свойства, являются следующие величины:

высота призмы h;
стороны основания a_i, где i = 1,...,n;
длины боковых ребер b_i.

Высотой фигуры называется длина перпендикулярного отрезка, которые соединяет основания. По сути, высота - это расстояние между n-угольниками.

Помимо линейных параметров призмы, в задачах по геометрии иногда необходимо знать значения ее двугранных углов, чтобы однозначно описать свойства. Двугранные углы бывают двух видов:

между боковыми параллелограммами;
между параллелограммом и основанием.

Теорема Пифагора для прямоугольного треугольника позволяет связать значения двугранных углов с линейными параметрами фигуры.

Какие бывают фигуры класса призм?

Выше была приведена шестиугольная призма. Рисунок ниже показывает, как выглядит треугольная призма. То есть первой классификацией фигур изучаемого класса является количество сторон основания. Если это количество будет стремиться к бесконечности, то мы получим цилиндрическую поверхность.

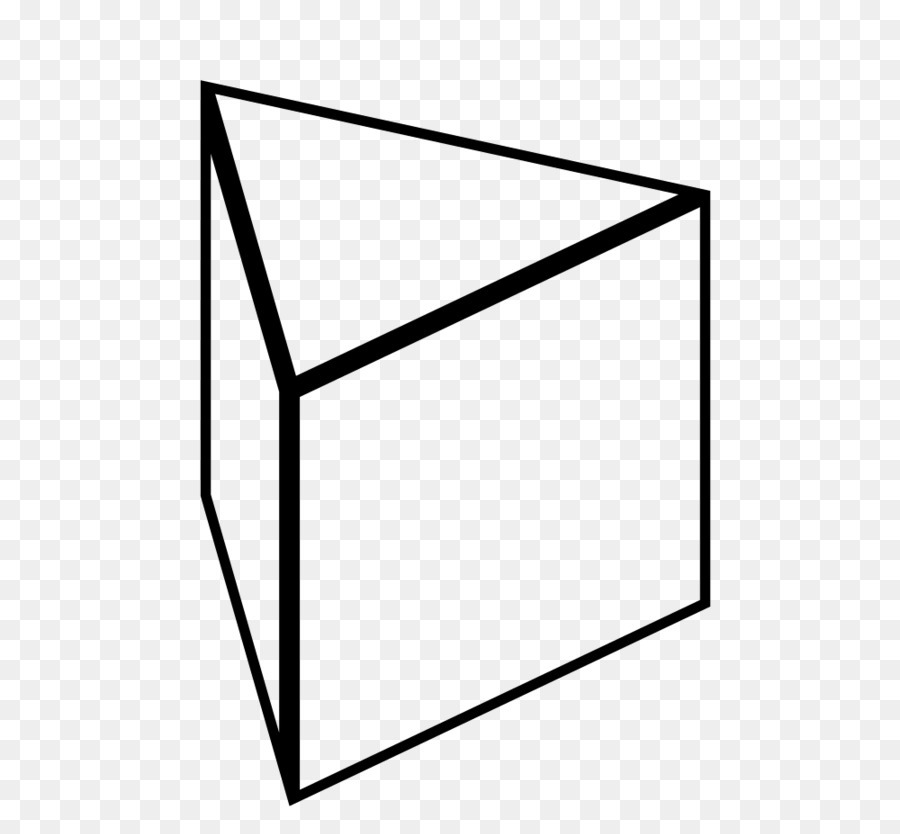
Второй тип классификации зависит от формы боковых сторон. Выше было сказано, что они являются параллелограммами. Однако, если эти параллелограммы одновременно будут прямоугольниками или квадратами, то такая фигура называется прямой призмой. В противном случае говорят о косоугольной или наклонной фигуре. Как выглядит прямая и наклонная четырехугольные призмы, можно увидеть на рисунке ниже.

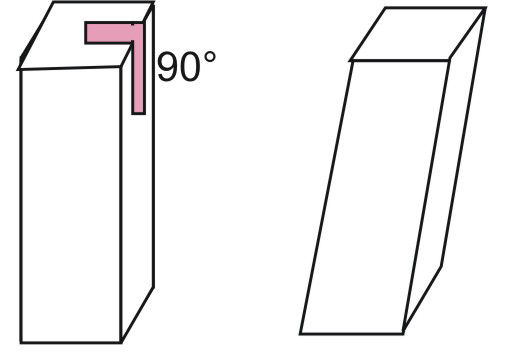
Заметим, что у прямых призм длины всех боковых ребер b_i равны между собой и равны высоте h.

Третья классификация призм базируется на форме их основания. Оно может быть вогнутым или выпуклым, соответственно призма называется вогнутой и выпуклой.

Наконец, самой важной классификацией является разделение всех фигур на призмы правильные и неправильные. Первые являются прямыми и образованы основаниями с одинаковыми сторонами и углами. Среди всех фигур четырехугольная правильная призма имеет собственное название - прямоугольный параллелепипед. Если у этого параллелепипеда все стороны равны, то он называется кубом.

Правильные призмы удобно изучать в плане таких свойств, как площадь поверхности и объем.

Площадь поверхности

Для рассмотрения вопроса поверхности призмы часто прибегают к изучению ее развертки. Для любой фигуры изучаемого класса развертка состоит из n параллелограммов и 2-х плоских n-угольников. Сложив площади всех граней, мы получим всю поверхность фигуры. Ниже показан пример развертки правильной пятиугольной призмы.

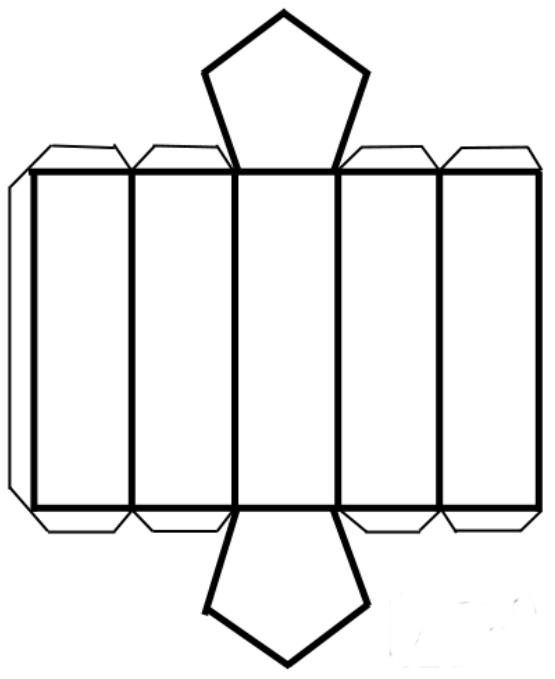
Для правильных призм можно записать общую формулу для площади S их поверхности:

S = n/2*a²*ctg(pi/n) + n*a*h.

Первое слагаемое в выражении является площадью обоих оснований, второе слагаемое - это площадь боковых граней. Площадь S правильной фигуры является функцией двух параметров: стороны основания a и высоты фигуры h.

Объем фигуры

Объемом называется величина, которая отражает свойство вещества заполнять пространство. Независимо от вида призмы, ее объем рассчитывается по следующей формуле: