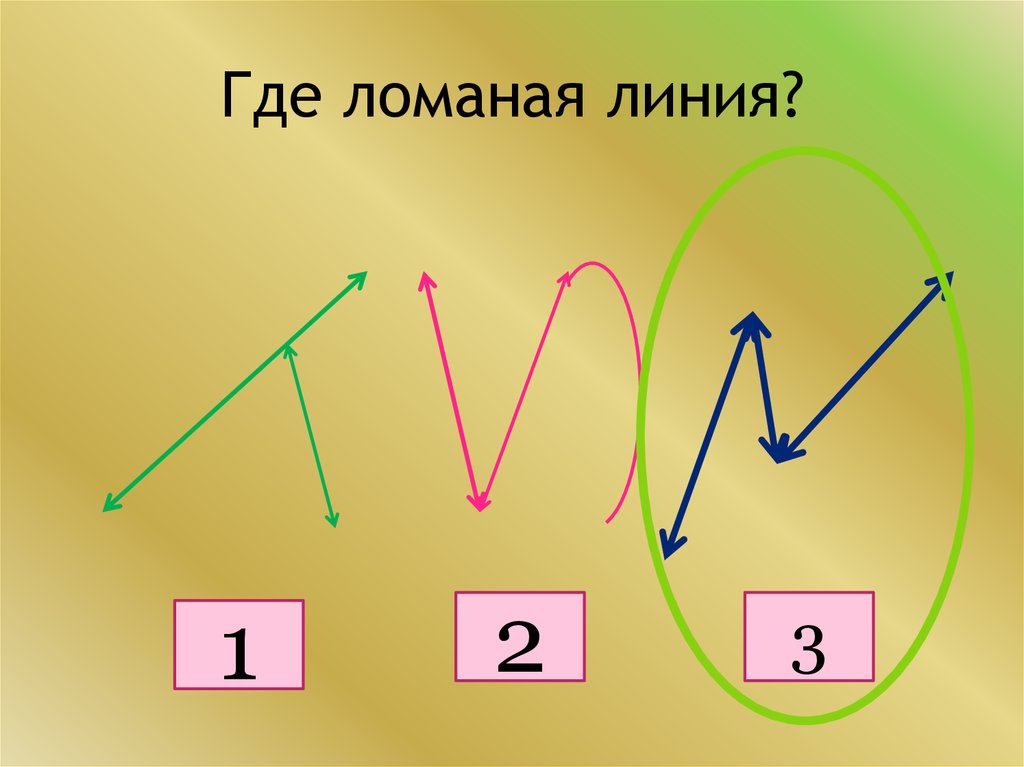
Что такое ломаная линия

Ломаная линия - это последовательность связанных между собой отрезков на плоскости или в пространстве. Она состоит из звеньев и вершин. Рассмотрим подробнее, что это такое.

Определение ломаной линии

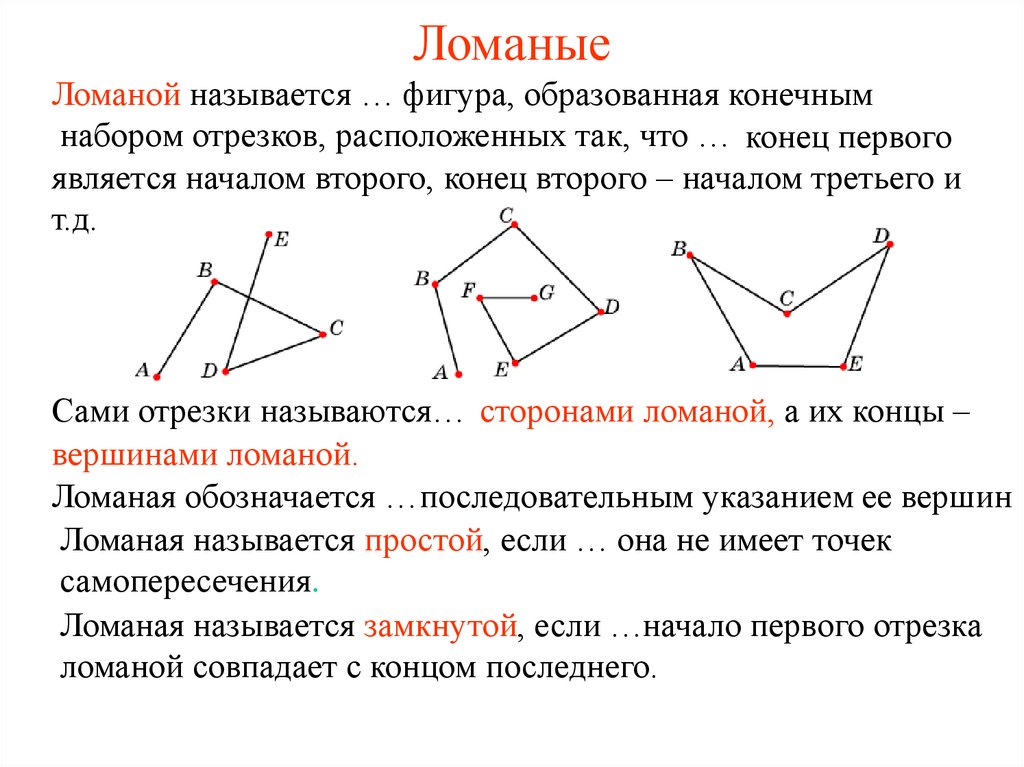
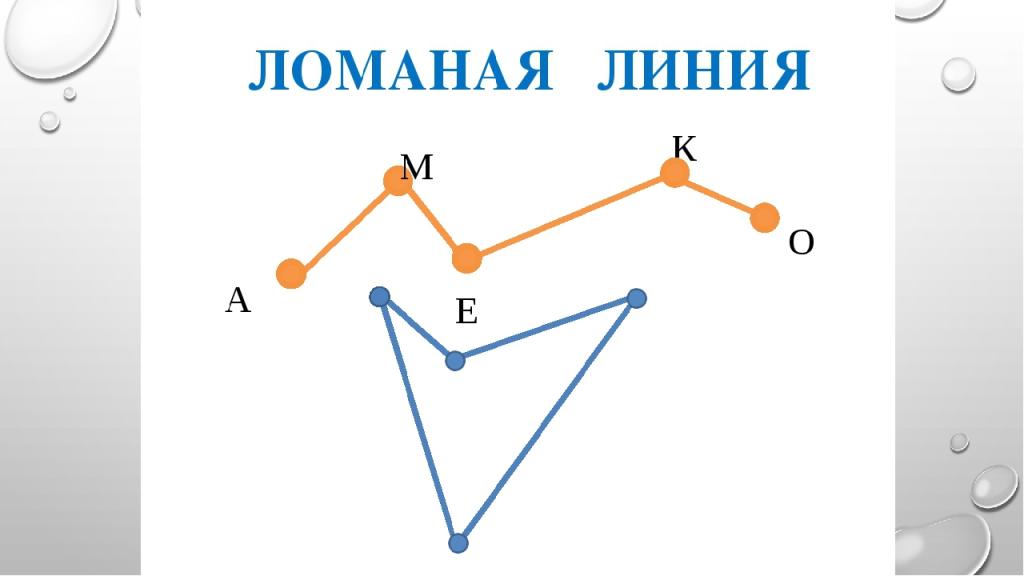
Ломаная линия представляет собой геометрическую фигуру, состоящую из отрезков прямых линий, соединенных последовательно так, что конец одного отрезка является началом следующего. Такие отрезки называют звеньями ломаной линии, а точки их соединения - вершинами.

Например, на рисунке изображена ломаная ABCDEF, состоящая из пяти звеньев: AB, BC, CD, DE и EF. У нее шесть вершин - точки A, B, C, D, E и F.

Таким образом, что такое ломаная - это последовательность связанных отрезков с общими конечными точками.

Виды ломаных линий

Различают несколько видов ломаных:

• По замкнутости: Замкнутые - начальная и конечная вершины совпадают Незамкнутые - начальная и конечная вершины разные
• По самопересечению: Самопересекающиеся - есть точки пересечения звеньев внутри ломаной Несамопересекающиеся - звенья не пересекаются

Например:

• Ломаная ABCDEF - незамкнутая и несамопересекающаяся
• Ломаная ANBMC - замкнутая и самопересекающаяся

Вычисление длины ломаной линии

Длиной ломаной линии называется сумма длин всех ее звеньев. Обозначается через L.

Например, пусть ломаная состоит из трех звеньев длиной 3 см, 5 см и 7 см. Тогда ее длина равна:

L = 3 см + 5 см + 7 см = 15 см

Для замкнутой ломаной без самопересечений длина называется периметром и обозначается буквой P.

Таким образом, длина ломаной вычисляется как сумма длин всех ее отрезков-звеньев.

Применение ломаных линий

Ломаные линии широко используются:

• В геометрии - для приближенного изображения кривых линий, вычисления площадей и объемов
• В инженерных расчетах - для моделирования конструкций сложной формы
• В компьютерной графике - для построения изображений
• На графиках в математике и физике - для отображения различных зависимостей

Ломаные широко используются благодаря простоте задания и вычислений. При увеличении числа звеньев ломаная может с заданной точностью приближать произвольную кривую.

Интересные факты о ломаных

• Самая известная ломаная - пятиконечная звезда. Это замкнутая самопересекающаяся пятиугольная ломаная.
• Многоугольник - это частный случай ломаной, у которой нет самопересечений и звенья образуют замкнутый контур.
• При построении графиков функций в математике используются ломаные для соединения точек графика.
• Траектория движения точки может быть апроксимирована ломаной линией, составленной из отрезков между последовательными положениями.

Ломаные линии, несмотря на простоту, демонстрируют удивительное разнообразие форм и свойств. Они широко используются в науке, технике и искусстве.

Построение ломаной линии

Для построения ломаной линии необходимо задать последовательность точек - вершин ломаной. Эти точки соединяются отрезками прямых линий. Получившиеся отрезки и будут звеньями ломаной.

Например, для построения ломаной ADBCE зададим координаты ее вершин:

• A(1;2)
• B(3;4)
• C(5;3)
• D(4;1)
• E(2;0)

Затем последовательно соединим эти точки отрезками. Получится искомая ломаная ADBCE, состоящая из звеньев AB, BC, CD, DE и EA.

Что такое ломаная в пространстве

Ломаная линия может быть определена не только на плоскости, но и в трехмерном пространстве. Что же представляет собой пространственная ломаная?

Это последовательность отрезков в пространстве, соединенных своими концами. Каждый отрезок задается координатами своих вершин. При этом отрезки могут быть расположены произвольно в пространстве.

Выпуклые и невыпуклые ломаные

Среди ломаных различают выпуклые и невыпуклые.

• Выпуклая ломаная - такая ломаная, внутри которой располагается выпуклый многоугольник, образованный ее звеньями.
• Невыпуклая ломаная - ломаная, внутри которой есть точки, не принадлежащие выпуклому многоугольнику, образованному ее звеньями. Такие точки называются внутренними.

На рисунке слева показана выпуклая ломаная ABCDEF, у нее нет внутренних точек. А ломаная KLMNOP является невыпуклой, точка Q - ее внутренняя точка.

Приближение кривых к ломаным

Благодаря гибкости формы, ломаные линии могут использоваться для приближенного изображения кривых на плоскости и в пространстве. Это одно из важных применений ломаных в геометрии и инженерной практике.

Процесс замены кривой ломаной называется аппроксимацией. С увеличением числа звеньев ломаная все точнее будет приближать форму кривой.

На рисунке показан пример приближения кривой ABCD ломаными линиями с разным количеством звеньев. Ломаная 3 приближает кривую точнее всех.

Ломаные линии в компьютерной графике

В компьютерной графике ломаные линии используются повсеместно для построения изображений. Преимущество ломаных в том, что они задаются простыми математическими формулами и легко обрабатываются компьютером.

С помощью отрезков и их комбинаций можно смоделировать сложные объекты. Например, круги и окружности строятся из большого числа коротких звеньев ломаной. При визуализации 3D-моделей их поверхность тоже аппроксимируется многогранником, ребра которого образуют ломаные.

Ломаные в инженерных расчетах

В строительстве и машиностроении при расчетах конструкций используется идея замены криволинейных участков ломаными. Это позволяет упростить математическое моделирование.

Например, для расчета прочности рамы или балки со сложным профилем, этот профиль аппроксимируют ломаной линией. А затем рассчитывают уже модель с ломаным контуром, что гораздо проще.

Ломаные на графиках функций

В математике и физике графики различных зависимостей часто строятся с использованием ломаных линий. Это связано с тем, что функции задаются таблично или опытным путем.

Полученные значения соединяются отрезками, в результате получается ломаная линия графика. Увеличивая число точек, можно с произвольной точностью приблизить график функции.

Ломаные в искусстве

В изобразительном искусстве ломаные линии используют для создания ощущения динамики и незавершенности. Особенно часто применяются ломаные с резкими углами.

Яркий пример - знаменитая картина Ван Гога “Звездная ночь”, где завихрения на небе переданы при помощи ломаных линий.

В архитектуре и дизайне ломаные формы придают зданиям и предметам выразительность. Это могут быть крыши, арки, различные элементы в интерьере.