История возникновения
Средоточием всех наук считается философия, так как именно она включала в себя первые ростки литературы, астрономии, литературы, естествознания, математики и прочих направлений. С течением времени каждая область развивалась самостоятельно, математика не стала исключением. Первым «намеком» на анализ считается теория разложения на бесконечно малые величины, к которой пытались подступиться многие умы, однако она носила туманный характер и не имела под собой базы. Это связано с привязанностью к старой школе науки, которая была строга в своих формулировках.
Исаак Ньютон был очень близок к тому, чтобы сформировать основы, но опоздал. В итоге своему появлению как обособленной системе математический анализ обязан философу Готфриду Лейбницу. Именно он в работах представил научному миру такие понятия, как минимум и максимум, точки перегиба и выпуклости графика функции, сформулировал основы дифференциального исчисления. С этого момента математику официально разделяют на элементарную и высшую.
Математический анализ. Наши дни
Любая специальность, будь она технической или гуманитарной, включает в курс обучения анализ. Глубина изучения разнится, но суть остается неизменной. Несмотря на всю «абстрактность», он является одним из столпов, на котором держится естествознание в современном его понимании. С его помощью получили развитие физика и экономика, он способен описать и спрогнозировать деятельность фондовой биржи, помочь в построении оптимального портфеля акций. Введение в математический анализ базируется на элементарных понятиях:
- множества;
- основные операции над множествами;
- свойства операций над множествами;
- функции (иначе – отображения);
- типы функций;
- последовательности;
- числовые прямые;
- предел последовательности;
- свойства пределов;
- непрерывность функции.
Стоит выделить отдельно такие понятия, как множество, точка, прямая, плоскость. Все они не имеют определений, так как являются базовыми понятиями, на которых строится вся математика. Все, что можно сделать в процессе работы – это пояснить, что именно они означают в отдельно взятых случаях.
Предел как продолжение
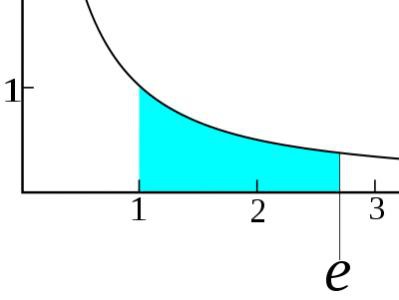
К основам математического анализа относится предел. На практике он представляет собой величину, к которой стремится последовательность или функция, подходит сколь угодно близко, но не достигает ее. Обозначается он как lim, рассмотрим частный случай предела функции: lim (x-1)= 0 при х→1. Из этого простейшего примера видно, что при х→1 вся функция стремится к 0, так как если подставить предел в саму функцию, то получим (1-1)=0. Подробнее, от элементарных до усложненных частных случаев, информация изложена в своеобразной «Библии» анализа – работах Фихтенгольца. Там рассматривается в разрезе математический анализ, пределы, их вывод и дальнейшее применение. Например, вывод числа e (константа Эйлера) был бы невозможен без теории пределов. Несмотря на динамическую абстрактность теории, пределы активно используются на практике все в той же экономике и социологии. Например, без них не обойтись при начислении процентов по банковскому вкладу.