Чему равна гравитационная постоянная?
После изучения курса физики в головах у учащихся остаются всевозможные постоянные и их значения. Тема гравитации и механики не становится исключением. Чаще всего ответить на вопрос о том, какое значение имеет гравитационная постоянная, они не могут. Но всегда однозначно ответят, что она присутствует в законе всемирного тяготения.
Из истории гравитационной постоянной
Интересно, что в работах Ньютона нет такой величины. Она появилась в физике существенно позже. Если быть конкретнее, то только в начале девятнадцатого века. Но это не значит, что ее не было. Просто ученые ее не определили и не узнали ее точное значение. Кстати, о значении. Гравитационная постоянная постоянно уточняется, поскольку является десятичной дробью с большим количеством цифр после запятой, перед которой стоит ноль.
Именно тем, что эта величина принимает такое маленькое значение, объясняется то, что действие сил гравитации незаметно на небольших телах. Просто из-за этого множителя сила притяжения оказывается ничтожно маленькой.
Впервые опытным путем установил значение, которое принимает гравитационная постоянная, физик Г. Кавендиш. И случилось это в 1788 году.

В его опытах использовался тонкий стержень. Он был подвешен на тоненькой проволоке из меди и имел длину около 2 метров. К концам этого стержня были прикреплены два одинаковых свинцовых шара диаметром 5 см. Рядом с ними были установлены большие свинцовые шары. Их диаметр был уже 20 см.
При сближении больших и маленьких шаров наблюдался поворот стержня. Это говорило об их притяжении. По известным массам и расстоянию, а также измеренной силе закручивания удалось достаточно точно узнать, чему равно гравитационное постоянное.
А началось все со свободного падения тел
Если поместить в пустоту тела разной массы, то они упадут одновременно. При условии их падения с одинаковой высоты и его начала в один и тот же момент времени. Удалось рассчитать ускорение, с которым все тела падают на Землю. Оно оказалось приблизительно равно 9,8 м/с2.
Ученые установили, что сила, с которой все притягивается к Земле, присутствует всегда. Причем это не зависит от высоты, на которую перемещается тело. Один метр, километр или сотни километров. Как бы далеко ни находилось тело, оно будет притягиваться к Земле. Другой вопрос в том, как ее значение будет зависеть от расстояния?
Именно на этот вопрос нашел ответ английский физик И. Ньютон.
Уменьшение силы притяжения тел с их отдалением
Для начала он выдвинул предположение о том, что сила тяжести убывает. И ее значение находится в обратной зависимости от расстояния, возведенного в квадрат. Причем это расстояние нужно отсчитывать от центра планеты. И провел теоретические расчеты.
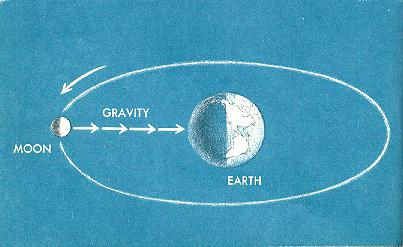
Потом этот ученый воспользовался данными астрономов о движении естественного спутника Земли — Луны. Ньютон рассчитал, с каким ускорением она вращается вокруг планеты, и получил те же результаты. Это свидетельствовало о правдивости его рассуждений и позволило сформулировать закон всемирного тяготения. Гравитационная постоянная в его формуле пока отсутствовала. На этом этапе было важно определить зависимость. Что и было сделано. Сила тяжести уменьшается обратно пропорционально расстоянию от центра планеты, возведенному в квадрат.
К закону о всемирном тяготении
Ньютон продолжил размышления. Поскольку Земля притягивает Луну, то и она сама должна притягиваться к Солнцу. Причем сила такого притяжения тоже должна подчиняться описанному им закону. А потом Ньютон распространил его на все тела вселенной. Поэтому и название закона включает слово «всемирное».
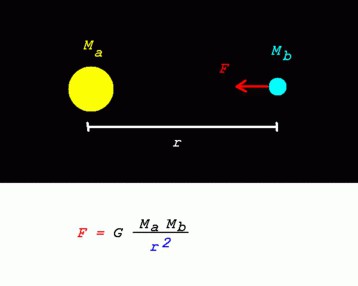
Силы всемирного тяготения тел определяются как пропорционально зависящие от произведения масс и обратные квадрату расстояния. Позже, когда был определен коэффициент, формула закона приобрела такой вид:
- Fт = G (m1 *х m2) : r2.
В ней введены такие обозначения:
| Сила тяготения | Fт |
| Гравитационная постоянная | G |
| Массы тел | m1, m2 |
| Расстояние между телами | r |
Формула гравитационной постоянной вытекает из этого закона:
- G = (Fт Х r2) : (m1 х m2).
Значение гравитационной постоянной
Теперь настал черед конкретных чисел. Поскольку ученые постоянно уточняют это значение, то в разные годы были официально приняты разные числа. К примеру, по данным за 2008 год гравитационная постоянная равна 6,6742 х 10-11 Нˑм2/кг2. Прошло три года - и константу пересчитали. Теперь гравитационная постоянная равна 6,6738 х 10-11 Нˑм2/кг2. Но для школьников в решении задач допустимо ее округление до такой величины: 6,67 х 10-11 Нˑм2/кг2.
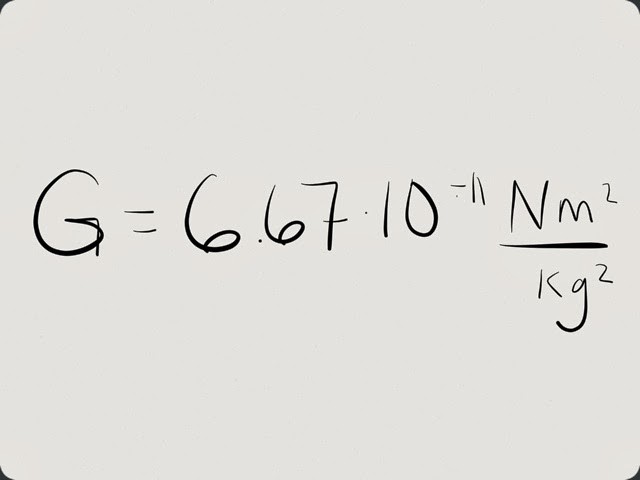
В чем физический смысл этого числа?
Если в формулу, которая дана для закона всемирного тяготения, подставить конкретные числа, то получится интересный результат. В частном случае, когда массы тел равны 1 килограмму, а расположены они на расстоянии 1 метра, сила тяготения оказывается равной самому числу, которое известно для гравитационной постоянной.
То есть смысл гравитационной постоянной заключается в том, что она показывает, с какой силой будут притягиваться такие тела на расстоянии одного метра. По числу видно, насколько мала эта сила. Ведь она в десять миллиардов меньше единицы. Ее даже невозможно заметить. Даже при увеличении тел в сотню раз результат существенно не изменится. Он по-прежнему останется гораздо меньше единицы. Поэтому становится понятно, отчего сила притяжения заметна только в тех ситуациях, если хотя бы одно тело имеет огромную массу. Например, планета или звезда.
Как связана гравитационная постоянная с ускорением свободного падения?
Если сравнить две формулы, одна из которых будет для силы тяжести, а другая для закона тяготения Земли, то можно увидеть простую закономерность. Гравитационная постоянная, масса Земли и квадрат расстояния от центра планеты составляют коэффициент, который равен ускорению свободного падения. Если записать это формулой, то получится следующее:
- g = (G х M) : r2.
Причем в ней используются такие обозначения:
| Масса Земли | M |
| Радиус Земли | r |
Кстати, гравитационную постоянную можно найти и из этой формулы:
- G = (g х r2) : M.
Если требуется узнать ускорение свободного падения на некоторой высоте над поверхностью планеты, то пригодится такая формула:
- g = (G х M) : (r + н)2, где н — высота над поверхностью Земли.
Задачи, в которых требуется знание гравитационной постоянной
Задача первая
Условие. Чему равно ускорение свободного падения на одной из планет Солнечной системы, например, на Марсе? Известно, что его масса 6,23·1023 кг, а радиус планеты 3,38·106 м.
Решение. Нужно воспользоваться той формулой, которая была записана для Земли. Только подставить в нее значения, данные в задаче. Получится, что ускорение свободного падения будет равно произведению 6,67 х 10-11 и 6,23 х 1023, которое потом нужно разделить на квадрат 3,38·106. В числителе получается значение 41,55 х 1012. А в знаменателе будет 11,42 х 1012. Степени сократятся, поэтому для ответа достаточно только узнать частное двух чисел.
Ответ: 3,64 м/с2.
Задача вторая
Условие. Что нужно сделать с телами, чтобы уменьшить их силу притяжения в 100 раз?
Решение. Поскольку массу тел изменять нельзя, то сила будет уменьшаться за счет удаления их друг от друга. Сотня получается от возведения в квадрат 10. Значит, расстояние между ними должно стать в 10 раз больше.
Ответ: отдалить их на расстояние, превышающее изначальное в 10 раз.
