Что такое египетская система счисления? История, описание, примеры

С непозиционной египетской системой счисления, которая употреблялась в Древнем Египте, нас наглядно знакомят немногие сохранившиеся папирусы. Примеры задач и их решения в них настолько интересны, что остается только сожалеть, что их так мало.

Из них видно, что математика и египетская система счисления были тесно связаны с хозяйственными нуждами и практическим применением. Каждый год после разлива Нила приходилось восстанавливать строения, заново межевать земельные наделы, рассчитывая площадь и границы, вести учет урожая, календарь.

Что такое позиционная и непозиционная системы счислений?

Ответ таится в самом названии. Если позиция цифры влияет на результат вычислений, перед нами позиционная система чисел, если нет – непозиционная.

Если мы пишем 12 – это двенадцать, а с теми же цифрами 21 – это двадцать один. По египетской системе счисления: чтобы написать 12, понадобится использовать два раза символ единицы и один раз символ десятки, а 21 будет выглядеть как один знак единицы и два знака десятки, то есть всего надо написать три знака.

К непозиционным относятся: знакомая нам римская система, в которой цифры обозначались римскими буквами, славянская система, где также каждая буква обозначала какую-то цифру или число. Римская система справлялась со своими функциями в Западной Европе до 16 века.

Используемая нами система счисления в современной жизни - позиционная десятичная система.

Непозиционные системы хорошо подходили для выполнения простых арифметических действий, так как сложные вычисления предполагали громоздкие записи, что не мешало в Древнем Египте успешному развитию алгебры и геометрии.

Как считали египтяне?

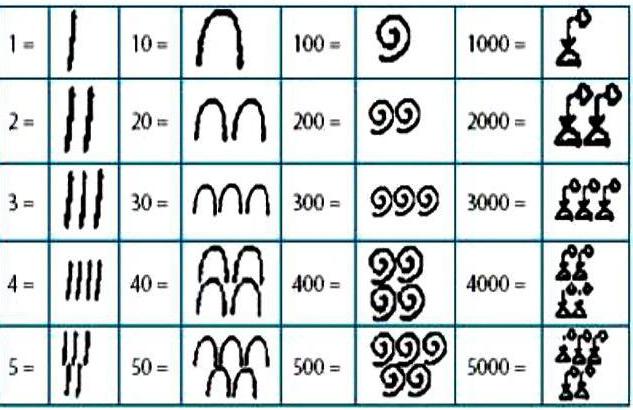
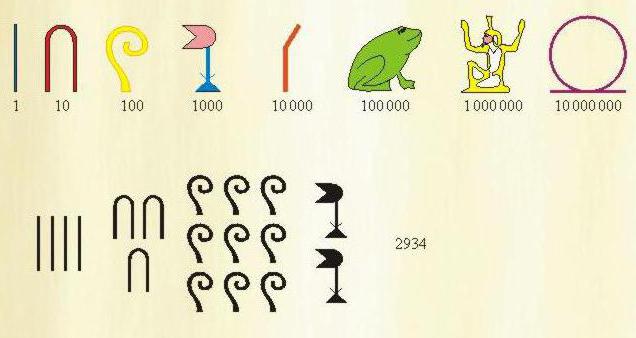
Что это такое – египетская система счисления? Чтобы написать какое-либо число, использовали иероглифы, обозначавшие определенные числа, сумма которых равнялась нужному значению.

Специальные обозначения имелись для чисел 1, 10, 100, 1000, 10000, 100000, 1000000. При написании нужного числа каждое обозначение использовалось до 9 раз. Запись в египетской системе счисления шла по возрастанию: вначале единицы, потом десятки, сотни и так далее.

Причем писали, как правило, справа налево, но можно было и слева направо, сумма от этого не менялась. Использовалось и вертикальное написание, но тогда отсчет шел сверху вниз.

Использовалось два способа написания:

1. Иероглифический, в котором употреблялись принятые иероглифы.
2. Иератический, который являлся более схематичным и удобным на практике.

Экскурс в историю

История египетской системы счисления возникла в глубокой древности, первые рукописи с цифрами относятся ко второму тысячелетию до нашей эры. Денег тогда не было, поэтому система использовалась как для невероятных по сложности и величию математических задач, так и для решения ежедневных бытовых вопросов.

Ведь знание математики использовалось и при межевании земель, и при построении календарей, карт в астрономии, мореплавании, при строительстве дворцов, каналов и военных укреплений.

Египетская непозиционная система счисления применялась до 10 века нашей эры.

Она имела и мистическое значение, тайну которого унесли с собой жрецы, но частично приоткрыл миру Пифагор. У него есть труды, в которых он описывает символические значения, которые придаются цифровым иероглифам, написанные им после пребывания в Египте. Поэтому относят их описание к египетской системе счисления.

Сохранилось всего несколько папирусов тех времен, по которым можно понять, что уровень математики был высокий. Достоверно известно, что греки изучали древнеегипетскую математику. Одним из сокровенных знаний является египетская непозиционная система счисления.

Папирус Ахмеса

Папирус Ахмеса датируется 1650 г. до н.э., содержит 84 математические задачи. Он был найден в Фивах, хранится в Британском музее.

Все задачи в папирусе рассмотрены на конкретных примерах египетской системы счисления. В них показываются примеры расчетов с дробями, с целыми числами, делением и умножением.

Даны расчеты для нахождения площадей геометрических фигур: четырехугольника, круга, треугольника.

Сведения из папируса доказывают, что египетские математики умели извлекать корень, составлять арифметическую и геометрическую прогрессию, уравнения с неизвестными.

Аликвотные дроби

Интересно, что в расчетах использовались только аликвотные дроби, в которых числитель равнялся единице и обозначался таким знаком, а под ним писались значения знаменателя, а все другие дроби для расчетов вначале нужно было разложить до аликвотных. Но использовались и имели специальное обозначение дроби 2/3 и 3/4.

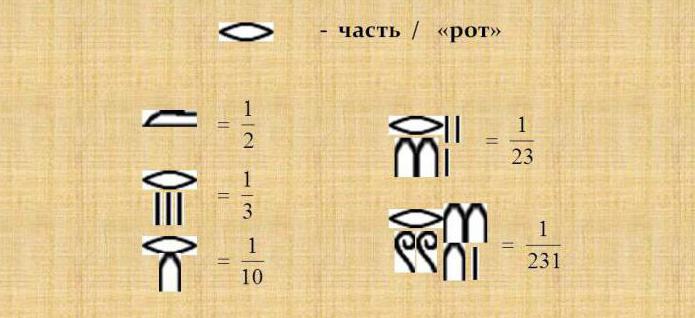
Для приведения обычных дробей в состояние аликвотных по египетской системе счисления нужно было потрудиться:

4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2+1/4 + 1/20

2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28

3/7 = 12/28 = 24/56 = 14/56+7/56+3/56 = 1/4+1/8+1/18+1/56.

Складывались дроби современным способом: приведением к общему знаменателю, для многих значений имелись многочисленные готовые таблицы.

Умножение

Египтяне узнавали нужный результат, не зная таблицы умножения, но используя знание о том, что, если один множитель увеличить в два раза, а другой уменьшить, то результат не изменится:

32*13=16*26=8*52=4*104=2*208=1*416

Интересно, что этот способ умножения был известен на Руси, и считалось, что он пришел из Древнего Египта, а в Европе его называли русским.

Папирус Голенищева

Благодаря стараниям ученого-египтолога В. С. Голенищева, в Москве хранится папирус еще на 200 лет древнее папируса писца Ахмеса. Ученый купил его во время своей работы в Фивах.

Он был написан иератическим способом, курсивом, в нем рассматривается 25 задач, дано их описание по египетской системе счисления и решение. Его длина более 5 м при ширине 7 см. К этим задачам нет никаких комментариев, как и в предыдущем папирусе, есть только математические расчеты.

Он показывает, что египтяне умели вычислять площади треугольника, трапеции, прямоугольника, круга, а также объёмы пирамиды, призмы, параллелепипеда, цилиндра и усечённой пирамиды с большой точностью, а многие формулы полностью совпадают с современными.

При египетской системе счисления было вычислено число «пи» 3,16, которое почти соответствовало современному значению 3,14, хотя в те времена повсеместно на Востоке использовалось значение, равное 3.

Все вещи – суть числа

Считается, Пифагор прожил в Египте 22 года, глубоко изучая геометрию, философию, мистику цифр. Те открытия, которые позднее делала Пифагорейская школа, вполне могли быть совершены еще в Древнем Египте.

Поэтому считается, что труды Пифагора о мистике цифр, которые он написал позже, основаны на тайных знаниях, полученных им от египетских жрецов. Они не брали на обучение иностранцев, попал он к ним по высокой протекции, после собеседования с главным жрецом, который счел его достойным быть посвященным в тайны.

Числа были живыми сущностями, отражающими свойства пространства, музыки, энергии. Все можно выразить через математику, описав формулами видимые явления предсказать невидимые, опираясь на логику и математические закономерности.

Высота, ширина основания, угол наклона пирамиды Хеопса в Египте соответствуют математическому правилу построения пирамиды Пифагора, что также подтверждает взаимосвязь сделанных им открытий и знаний, полученных от древнеегипетских жрецов, использовавших египетскую систему счисления.

Работая с цифрами, древние мыслители не только понимали суть вещей, но и могли воздействовать на них.

Изучая математику Древнего Египта, использующую египетскую систему счисления, можно только восхищаться тем, как много было открыто людям за тысячи лет до нашей эры.