Парадоксы Зенона Элейского - описание, значение и интересные факты

Парадоксы Зенона вводили в недоумение многих ученых и философов до 17 века. И до сих пор многие ученые спорят о бесконечности, структуре пространства и времени, хотя началось все с нескольких парадоксальных утверждений, ставящих поначалу в логический тупик любого умного человека.

История возникновения парадоксов Зенона

Зенон Элейский – философ Древней Эллады, ученик основателя Элейской школы – Парменида. Жил он с 515 по 450 год до нашей эры, о его жизни известно очень мало. Родился в городе Элее в южной части Италии. По утверждению Платона, Зенон побывал в Афинах и встретился с Сократом. Прославился благодаря своим апориям, в виде которых был сформулирован знаменитый парадокс Зенона. Апории Зенона представляют собой парадоксальные рассуждения, само же слово «апория» с греческого языка обозначает «безвыходность».

В древние времена современники насчитывали 40 парадоксальных утверждений, а до наших дней дошли только 9, наиболее известны - 4. Узнали об апориях Зенона благодаря трудам Аристотеля, а также благодаря таким философам, как Диоген Лаэртский, Платон, Филопон, Симпликий. Кстати, стоит сказать о самой Элейской школе, к которой Зенон принадлежал. Основные ее учения гласят, что любое изменение является иллюзией, бытие же является единым и не изменяется. Зенон говорил, что истинная реальность является вечной и неизменной, и постигнуть ее можно только с помощью разума и логики. Поэтому многие апории Зенона посвящены движению, в них он показывает, что движения (или изменения), с точки зрения логики, не существует.

Парадоксы о движении и времени

«Состязание Ахиллеса и черепахи» - один из самых известных парадоксов Зенона. Наверное, его знает каждый школьник. Существуют еще такие апории Зенона, как «Полет стрелы», «Дихотомия» и другие. Они посвящены движению, обсуждаемы и изучаются уже два тысячелетия. Им посвящены были многие исследования, и вплоть до 17 века мыслители не могли опровергнуть эту хитроумную логику.

Проблема решилась после идеи дифференциального исчисления, которую предложили Ньютон и Лейбниц. Там есть понятие «предел», так прояснилась разница между разбиением времени и разбиением на отрезки определенного пути. К тому же загадка разрешилась, когда ученые научились пользоваться бесконечно малыми величинами. Апории Зенона породили с тех пор множество различных вариаций. Кроме того, возможно, добавились некоторые детали. Мы перечислим сохранившиеся до наших дней парадоксы Зенона и кратко расскажем об их сути. Во всяком случае, попытаемся это сделать.

Парадокс Зенона об Ахиллесе и черепахе

Герой мифов Древней Греции Ахиллес соревнуется в скорости бега с черепахой. Условия таковы, что черепаха стартует немного дальше, Ахиллес находится от нее на расстоянии в 1000 шагов.

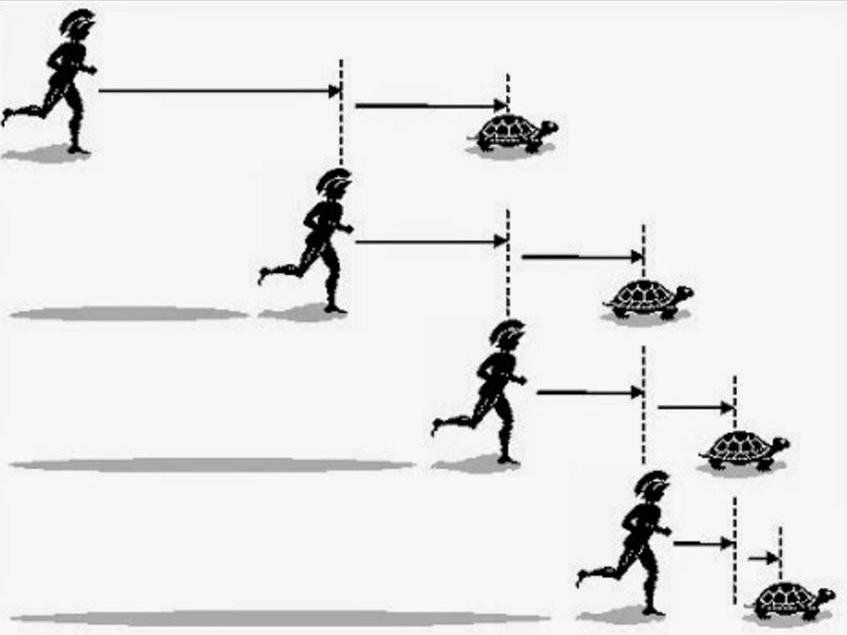
Чтобы догнать черепаху, Ахиллес должен достигнуть сначала места, с которого черепаха стартовала. Но как только он добежит до этого места, черепаха успеет проползти 100 шагов. Это расстояние, которое она проползла, еще предстоит преодолеть Ахиллесу, но к тому времени она уползет еще дальше на 10 шагов и так далее. Число таких отрезков, которые нужно преодолеть Ахиллесу, по утверждению Зенона, может быть бесконечным, ведь величина этих отрезков все время будет уменьшаться до бесконечно малых величин.

Выходит, если следовать такой логике, древнегреческий герой никогда не догонит черепаху. Парадокс Зенона заключается в существовании бесконечного количества бесконечно малых отрезков, но в реальной жизни бегун наверняка обгонит медлительное животное.

Летящая стрела

Этот парадокс получил название «Стрела». Это еще одна апория, которую Зенон сформулировал приблизительно следующими словами. Если что-либо пребывает в движении, то оно движется либо в том месте, которое оно занимает собой, либо оно движется там, где его нет. Но оно не способно двигаться в том месте, которое оно занимает. Так как в каждую секунду оно занимает полностью все это место. Но и в том месте, где его нет, оно не может двигаться. Следовательно, движение само по себе невозможно.

По утверждению Зенона, стрела, когда летит, одновременно пребывает в покое. Потому что в каждый момент она занимает одно и то же пространство, равное ей. То есть стрела пребывает в покое относительно места, где она находится в определенный промежуток времени. Получается, что летящая стрела неподвижна. Если она неподвижна в определенный момент, значит, она находится в покое и в другие моменты времени. И нет того момента, когда стрела двигалась.

Дихотомия

Парадокс, который будет приведен далее, имеет название «дихотомия». В переводе с греческого языка оно означает «разделение надвое», и дано оно Аристотелем. Эта апория изложена примерно по такому же принципу, как и парадокс Зенона об Ахиллесе и черепахе.

В оригинале говорится о бегуне, который не в состоянии даже стартовать, ведь движения, по мнению Зенона, не существует. Но есть еще и распространенный вариант про пересечение комнаты.

Чтобы пересечь комнату, нужно сначала пересечь половину комнаты. На это уйдет определенная единица времени. После этого останется определенное расстояние, нужно преодолеть половину его за еще одну единицу времени. Затем тот отрезок пути, что остался, нужно разделить еще надвое и пройти половину этого отрезка за то же время. Тогда опять остается определенное расстояние, половину которого надо пересечь. Получается, что комнату пересекать можно бесконечно.

Две колонны на стадионе

Две колонны людей, одинаковые по длине, двигаются параллельно с одинаковой скоростью в противоположных направлениях. По утверждению Зенона, время которое истечет, когда колонны будут проходить мимо друг друга, равно половине того времени, которое нужно одному человеку, чтобы пройти мимо всей колонны.

Разрешение парадоксов Зенона

Из четырех перечисленных апорий наибольшую известность получили первые три. Четвертая появилась из-за неправильного понимания природы относительного движения.

Все апории можно легко опровергнуть экспериментально. Ничего не мешает пересечь комнату, выпустить стрелу и обогнать черепаху.

Рассмотрим парадокс, связанный с пересечением комнаты. Конечно, если разделить расстояние надвое и пройти половину, на это уйдет определенное количество времени. Останется еще расстояние, которое тоже нужно поделить надвое и пройти половину. Но для этого времени понадобится в два раза меньше. Чем меньше становится расстояние, которое необходимо преодолеть, тем больше будет сокращаться время на его прохождение. Выходит, при пересечении комнаты в конце требуется неограниченное число бесконечно маленьких временных отрезков. Но если сложить все отрезки, получится определенное число – оно-то и будет временем, затраченным на пересечение комнаты. Получается, пересечь комнату вполне возможно за определенный промежуток времени. Это доказательство схоже с нахождением предела при дифференциальном исчислении. Древнегреческий философ Зенон ошибочно предполагал, что при прохождении бесконечно малых расстояний каждый раз требуется одно и то же время.

Что касается парадокса Зенона «Летящая стрела», еще Аристотель его раскритиковал, утверждая, что каждый момент времени не может быть неделимым сам по себе. Еще он говорил, что рассуждения Зенона о том, что если все занимающее равное себе место пребывает в покое, и если то, что пребывает в движении, всегда занимает в любой момент такое же место, то стрела неподвижна, ошибочны.

Квантовый эффект

Парадоксы Зенона были опровергнуты со временем многими учеными. Но они все же внесли определенный вклад в науку. В квантовой физике на сегодняшний момент есть такое понятие, как квантовый парадокс Зенона. Он заключается в том, что если наблюдать за нестабильной частицей, например, проводить измерения, проверять, распалась частица или нет, то возникает некоторое замедление радиоактивного распада.

Предполагается, что если непрерывно наблюдать за частицей, то она может вообще не распасться. В 90-х годах прошлого века этот квантовый эффект был подтвержден с помощью ряда экспериментов.