Знаменатель геометрической прогрессии: формулы и свойства

Геометрическая прогрессия, наряду с арифметической, является важным числовым рядом, который изучается в школьном курсе алгебры в 9 классе. В данной статье рассмотрим знаменатель геометрической прогрессии, и то, как его значение влияет на ее свойства.

Определение прогрессии геометрической

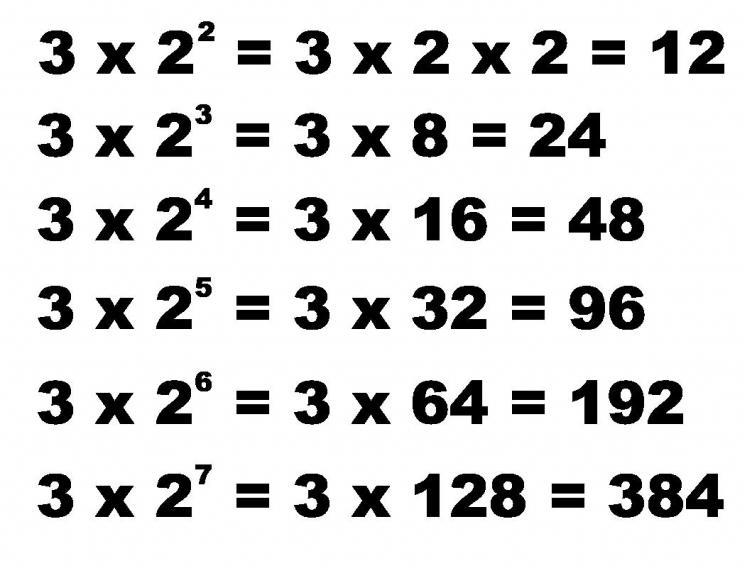
Для начала приведем определение этого числового ряда. Прогрессией геометрической называют такой ряд рациональных чисел, который формируется путем последовательного умножения его первого элемента на постоянное число, носящее название знаменателя.

Например, числа в ряду 3, 6, 12, 24, ... - это прогрессия геометрическая, поскольку если умножить 3 (первый элемент) на 2, то получим 6. Если 6 умножить на 2, то получим 12, и так далее.

Члены рассматриваемой последовательности принято обозначать символом a_i, где i - это целое число, указывающее на номер элемента в ряду.

Приведенное выше определение прогрессии можно записать на языке математики следующим образом: a_n = b^n-1 * a₁, где b - знаменатель. Проверить эту формулу легко: если n = 1, то b^1-1 = 1, и мы получаем a₁ = a_1. Если n = 2, тогда a_n = b * a₁, и мы снова приходим к определению рассматриваемого ряда чисел. Аналогичные рассуждения можно продолжить для больших значений n.

Знаменатель прогрессии геометрической

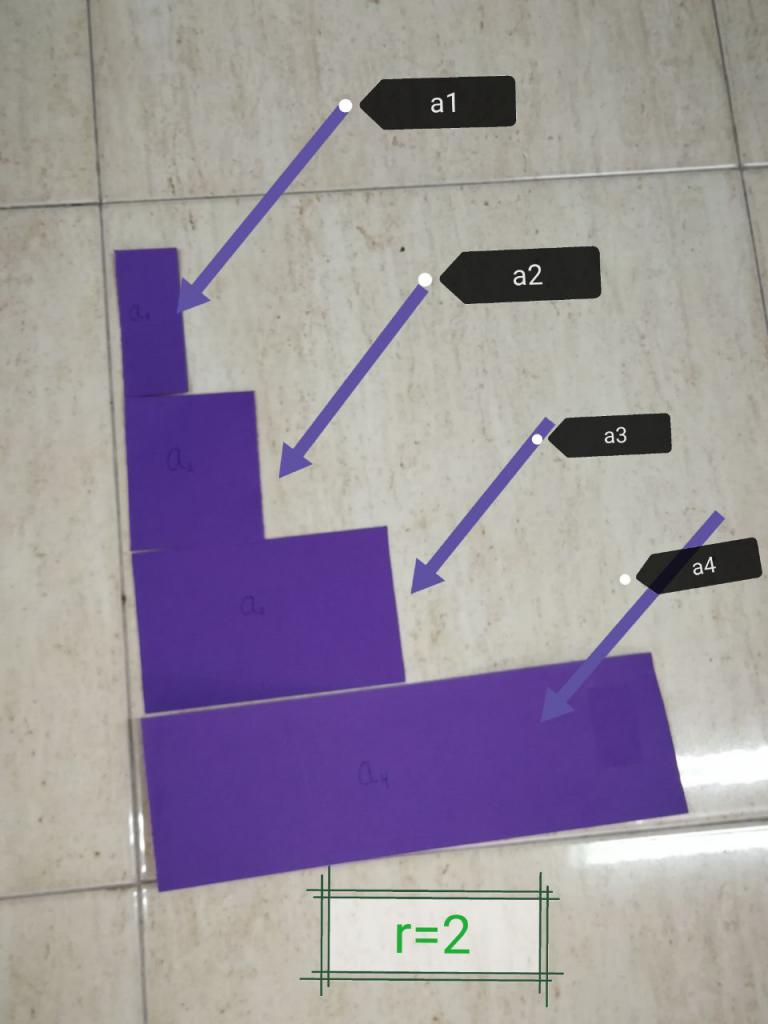
Число b полностью определяет, какой характер будет носить весь числовой ряд. Знаменатель b может быть положительный, отрицательный, а также иметь значение больше единицы или меньше. Все перечисленные варианты приводят к разным последовательностям:

• b > 1. Имеет место возрастающий ряд рациональных чисел. Например, 1, 2, 4, 8, ... Если элемент a₁ будет отрицательным, тогда вся последовательность будет возрастать только по модулю, но убывать с учетом знака чисел.
• b < -1. В этом случае речь идет о переменном ряде, то есть соседние элементы будут отличаться знаком. Например, 1, -2, 4, -8, 16, ...
• -1 < b < 1. Это особый случай, который имеет собственное название - убывающая бесконечно прогрессия геометрическая. Ее главное свойство состоит в том, что независимо от знака знаменателя, она стремится к некоторой конечной сумме при сложении бесконечного числа ее элементов.
• b = 1. Часто такой случай не называют прогрессией, поскольку имеет место обычный ряд одинаковых рациональных чисел. Например, -4, -4, -4.

Формула для суммы

Перед тем как перейти к рассмотрению конкретных задач с использованием знаменателя рассматриваемого вида прогрессии, следует привести важную формулу для суммы ее первых n элементов. Формула имеет вид: S_n = (bⁿ - 1) * a₁ / (b - 1).

Получить это выражение можно самостоятельно, если рассмотреть рекурсивную последовательность членов прогрессии. Также заметим, что в приведенной формуле достаточно знать только первый элемент и знаменатель, чтобы найти сумму произвольного числа членов.

Бесконечно убывающая последовательность

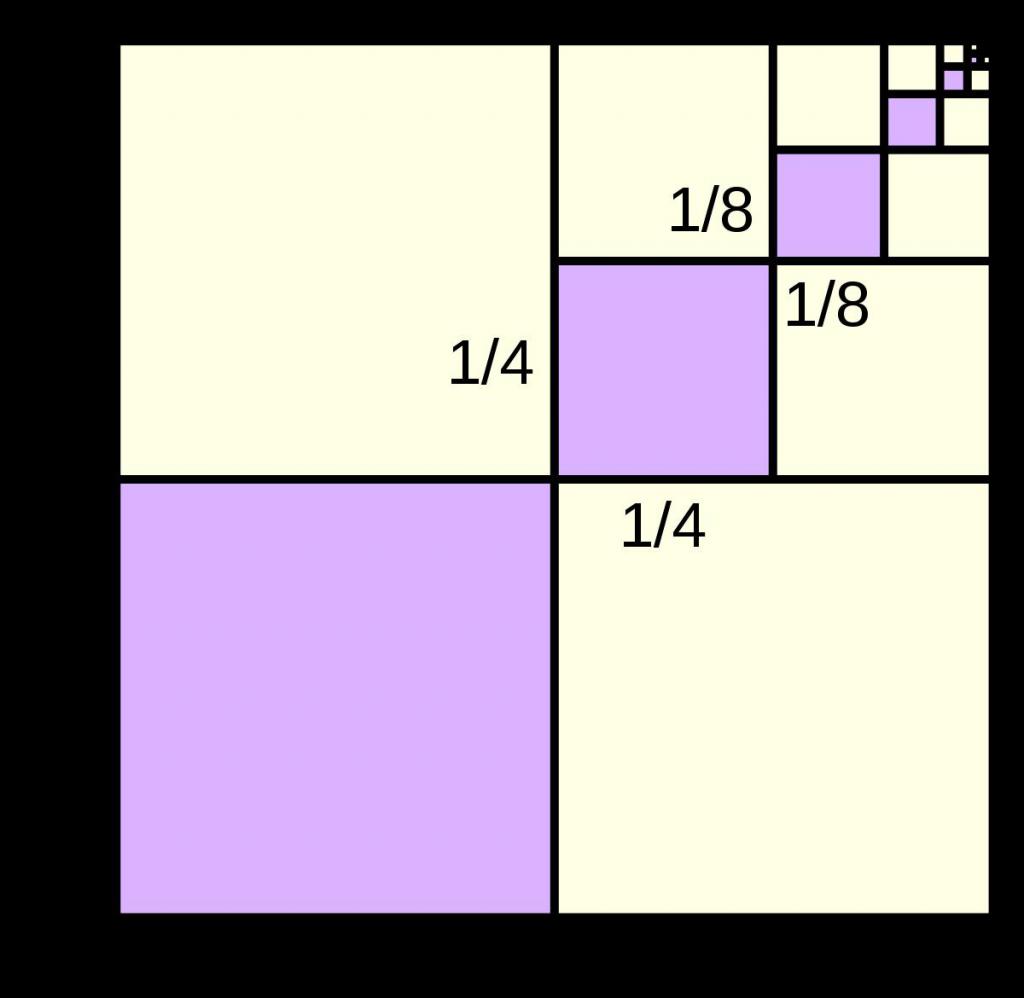
Выше было дано пояснение, что она собой представляет. Теперь, зная формулу для S_n, применим ее к этому числовому ряду. Так как любое число, модуль которого не превышает 1, при возведении в большие степени стремится к нулю, то есть b^∞ => 0, если -1 < b < 1 (|b| < 1), то общая формула для суммы преобразуется в следующее выражение: S_∞ = a₁ / (1 - b).

Поскольку разность (1 - b) всегда будет положительной, независимо от значения знаменателя, то знак суммы убывающей бесконечно прогрессии геометрической S_∞ однозначно определяется знаком ее первого элемента a₁.

Теперь рассмотрим несколько задач, где покажем, как применять полученные знания на конкретных числах.

Задача № 1. Вычисление неизвестных элементов прогрессии и суммы

Дана прогрессия геометрическая, знаменатель прогрессии 2, а ее первый элемент 3. Чему будут равны ее 7-й и 10-й члены, и какова сумма ее семи начальных элементов?

Условие задачи составлено достаточно просто и предполагает непосредственное использование вышеназванных формул. Итак, для вычисления элемента с номером n используем выражение a_n = b^n-1 * a₁. Для 7-го элемента имеем: a₇ = b⁶ * a_1, подставляя известные данные, получаем: a₇ = 2⁶ * 3 = 192. Аналогичным образом поступаем для 10-го члена: a₁₀ = 2⁹ * 3 = 1536.

Воспользуемся известной формулой для суммы и определим эту величину для 7-ми первых элементов ряда. Имеем: S₇ = (2⁷ - 1) * 3 / (2 - 1) = 381.

Задача № 2. Определение суммы произвольных элементов прогрессии

Пусть -2 равен знаменатель прогрессии в геометрической прогрессии b^n-1 * 4, где n - целое число. Необходимо определить сумму с 5-го по 10-й элемент этого ряда включительно.

Поставленная проблема не может быть решена непосредственно с использованием известных формул. Решить ее можно 2-мя различными методами. Для полноты изложения темы приведем оба.

Метод 1. Идея его проста: необходимо рассчитать две соответствующие суммы первых членов, а затем вычесть из одной другую. Вычисляем меньшую сумму: S₁₀ = ((-2)¹⁰ - 1) * 4 / (-2 - 1) = -1364. Теперь вычисляем большую сумму: S₄ = ((-2)⁴ - 1) * 4 / (-2 - 1) = -20. Отметим, что в последнем выражении суммировались только 4 слагаемых, поскольку 5-е уже входит в сумму, которую требуется вычислить по условию задачи. Наконец, берем разницу: S₅¹⁰ = S₁₀ - S₄ = -1364 - (-20) = -1344.

Метод 2. Перед тем, как подставлять цифры и считать, можно получить формулу для суммы между членами m и n рассматриваемого ряда. Поступаем абсолютно так же, как в методе 1, только работаем сначала с символьным представлением суммы. Имеем: Sⁿ_m = (bⁿ - 1) * a₁ / (b - 1) - (b^m-1 - 1) * a₁ / (b - 1) = a₁ * (bⁿ - b^m-1) / (b - 1). В полученное выражение можно подставлять известные числа и вычислять конечный результат: S¹⁰₅ = 4 * ((-2)¹⁰ - (-2)⁴) / (-2 - 1) = -1344.

Задача № 3. Чему равен знаменатель?

Пусть a₁ = 2, найдите знаменатель прогрессии геометрической, при условии, что ее бесконечная сумма составляет 3, и известно, что это убывающий ряд чисел.

По условию задачи нетрудно догадаться, какой формулой следует пользоваться для ее решения. Конечно же, для суммы прогрессии бесконечно убывающей. Имеем: S_∞ = a₁ / (1 - b). Откуда выражаем знаменатель: b = 1 - a₁ / S_∞. Осталось подставить известные значения и получить требуемое число: b = 1 - 2 / 3 = -1 / 3 или -0,333(3). Можно качественно проверить этот результат, если вспомнить, что для этого типа последовательности модуль b не должен выходить за пределы 1. Как видно, |-1 / 3| < 1.

Задача № 4. Восстановление ряда чисел

Пусть даны 2 элемента числового ряда, например, 5-й равен 30 и 10-й равен 60. Необходимо по этим данным восстановить весь ряд, зная, что он удовлетворяет свойствам прогрессии геометрической.

Чтобы решить задачу, необходимо для начала записать для каждого известного члена соответствующее выражение. Имеем: a₅ = b⁴ * a₁ и a₁₀ = b⁹ * a₁. Теперь разделим второе выражение на первое, получим: a₁₀ / a₅ = b⁹ * a₁ / (b⁴ * a₁) = b⁵. Отсюда определяем знаменатель, взяв корень пятой степени от отношения известных из условия задачи членов, b = 1,148698. Полученное число подставляем в одно из выражений для известного элемента, получаем: a₁ = a₅ / b⁴ = 30 / (1,148698)⁴ = 17,2304966.

Таким образом, мы нашли, чему равен знаменатель прогрессии bn, и геометрическую прогрессию b^n-1 * 17,2304966 = a_n, где b = 1,148698.

Где применяются прогрессии геометрические?

Если бы не существовало применения этого числового ряда на практике, то его изучение сводилось бы к чисто теоретическому интересу. Но такое применение существует.

Ниже перечислены 3 самых знаменитых примера:

• Парадокс Зенона, в котором ловкий Ахиллес не может догнать медленную черепаху, решается с использованием понятия убывающей бесконечно последовательности чисел.
• Если на каждую клетку шахматной доски класть зерна пшеницы так, что на 1-ю клетку положить 1 зерно, на 2-ю - 2, на 3-ю - 3 и так далее, то чтобы заполнить все клетки доски понадобится 18446744073709551615 зерен!
• В игре "Башня Ханоя", чтобы переставить диски с одного стержня на другой, необходимо выполнить 2ⁿ - 1 операций, то есть их число растет в геометрической прогрессии от количества используемых дисков n.