Свойства правильной треугольной пирамиды. Усеченная пирамида с треугольным основанием

Пирамида является одной из важных фигур, характеристики которой подробно изучают в старших классах школ на уроках стереометрии (раздел геометрии). В данной статье рассмотрим правильную треугольную пирамиду и свойства ее, такие как объем и площадь поверхности. Также кратко будет изучена усеченная пирамида с треугольным основанием.

Что значит пирамида треугольная правильная?

В стереометрии можно встретить следующее определение пирамиды: это пространственная фигура, которая состоит из двух видов граней - треугольников и одного многоугольника. Последний называется "основанием", а треугольники составляют боковую поверхность, поэтому именуются "боковыми гранями". Одна из вершин всех треугольников пересекается в одной точке, которая называется "вершиной пирамиды".

Правильная треугольная пирамида - это фигура класса многогранников, которая имеет в основании равносторонний треугольник. Если опустить из вершины ее перпендикулярный отрезок к основанию, то он пересечет его в геометрическом центре, то есть в точке пересечения медиан равностороннего треугольника. Пример этой фигуры показан ниже на рисунке.

Когда учитель в школе просит: "Перечислите свойства пирамиды треугольной правильной", то следует сказать, что изучаемая фигура образована четырьмя гранями и четырьмя вершинами. Боковые ее грани в общем случае представляют равносторонние (равные между собой) треугольники. Фигура имеет шесть ребер: три основания и три одинаковых боковых.

Линейные параметры пирамиды

В общем случае речь идет о четырех параметрах фигуры:

• сторона основания a;
• боковое ребро b;
• высота h;
• апофема h_b (высота бокового треугольника, опущенная на сторону основания из вершины пирамиды).

Продолжаем рассматривать свойства правильной треугольной пирамиды. Высота h с другими линейными параметрами связана следующими выражениями:

h = √(h_b² - a²/12);

h = √(b² - a²/3)

В свою очередь, боковое ребро b, апофема h_b и сторона a связаны таким равенством:

b² = a²/4 + h_b²

Поскольку имеется четыре показателя и три уравнения, то для однозначного определения свойств правильной пирамиды треугольной необходимо знать любые два из этих параметров.

Площадь и объем фигуры

Площадь изучаемой пирамиды представляет собой сумму площадей всех ее четырех треугольных сторон, причем три из них (боковые) равны между собой. Ниже изображена развертка этой фигуры, которая ясно показывает все грани пирамиды на плоскости.

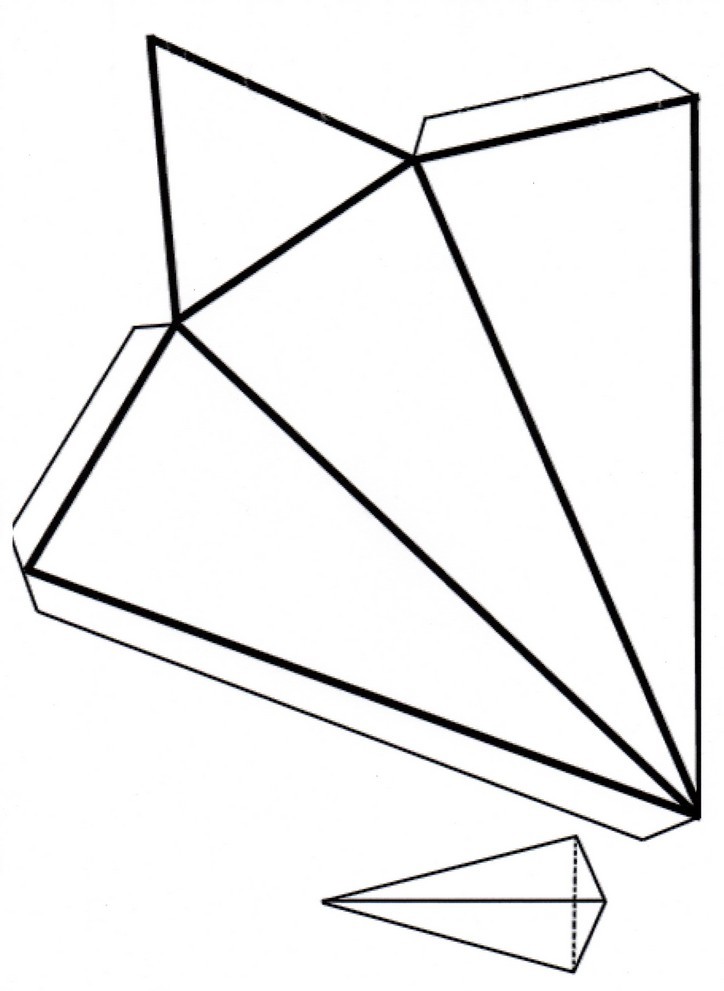
Для определения площадей треугольников воспользуемся универсальной формулой: любой треугольник имеет площадь, которая вычисляется как половина произведения его высоты на основание. Для треугольника основания имеем:

S_o = √3/4*a²

Площадь одной боковой грани S_b1 равна:

S_b1 = 1/2*a*h_b

Тогда площадь всей поверхности будет равна:

S = S_o + 3*S_b1 = √3/4*a² + 3/2*a*h_b

Объем фигуры можно рассчитать по общей формуле для многогранника класса пирамиды. Эта формула имеет вид:

V = 1/3*S_o*h

Поскольку формулу для площади основания мы привели выше, то объем изучаемой треугольной пирамиды вычисляется так:

V = √3/12*a² *h

Как видно из записанных выражений для V и S, свойства треугольной правильной пирамиды зависят от двух линейных параметров и однозначно рассчитываются из знания их значений.

Усеченная пирамида

Название этой фигуры говорит само за себя. Получается усеченная пирамида из обычной, если срезать ее верхнюю часть. При этом плоскость среза должна быть параллельна плоскости треугольного основания. Эта фигура показана ниже.

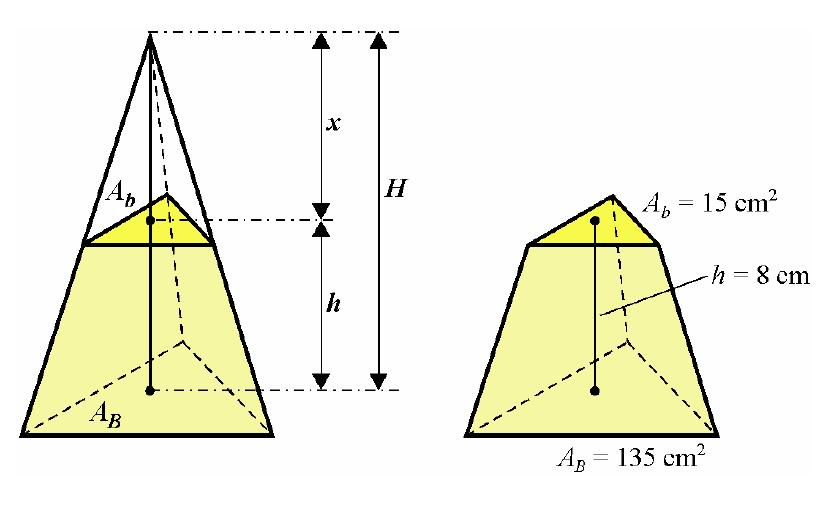
Из рисунка видно, что фигура образована двумя равносторонними треугольниками разных размеров. Они называются основаниями пирамиды. Боковая поверхность состоит из трех одинаковых равнобедренных трапеций. Таким образом, усеченная треугольная правильная пирамида кардинальным образом отличается от полной.

Важными свойствами правильной усеченной треугольной пирамиды являются площадь поверхности ее и объем. Формулы для их вычисления выглядят несколько сложнее, чем аналогичные выражения для полной фигуры. Здесь не будем вдаваться в подробности получения этих формул, а приведем их сразу:

S = 3/2*h_b*(a₁ + a₀) + √3/4*(a₁² + a₀²);

V = √3/12*h*(a₁²+a₀²+a₀*a₁)

Здесь a₁ и a₀ - стороны треугольников разных оснований, h - расстояние между основаниями, h_b - высота трапеции пирамиды. В формуле для S первое слагаемое соответствует площади боковой поверхности пирамиды, второе - это площадь двух оснований. Из записанных формул для S и V усеченной пирамиды видно, что для однозначного определения ее свойств необходимо знать три линейных параметра фигуры.