Кинетическая энергия - энергия движения тел

Потенциальная и кинетическая энергия позволяют охарактеризовать состояние любого тела. Если первая применяется в системах взаимодействующих объектов, то вторая связана с их движением. Эти виды энергии, как правило, рассматриваются тогда, когда сила, связывающая тела, независима от траектории движения. При этом важны только начальное и конечное их положения.

Общие сведения и понятия

Кинетическая энергия системы является одной из важнейших ее характеристик. Физики выделяют два вида такой энергии в зависимости от вида движения:

• поступательная;

• вращения.

Кинетическая энергия (Е_к) представляет собой разность между полной энергией системы и энергией покоя. Исходя из этого, можно сказать, что она обусловлена движением системы. Тело имеет ее только тогда, когда оно движется. В состоянии покоя объекта она равняется нулю. Кинетическая энергия любых тел зависит исключительно от скорости движения и их масс. Полная энергия системы находится в прямой зависимости от скорости ее объектов и расстояния между ними.

Основные формулы

В том случае, когда любая сила (F) действует на тело, находящееся в покое так, что оно приходит в движение, можно говорить о совершении работы dA. При этом величина этой энергии dE будет тем выше, чем больше совершается работы. В этом случае верно такое равенство: dA = dE.

С учетом пути, пройденного телом (dR) и его скорости (dU), можно воспользоваться 2 законом Ньютона, исходя из которого: F = (dU/dE)*m.

Вышеуказанный закон используется только тогда, когда имеется инерциальная система отсчета. Существует еще один важный нюанс, учитываемый при расчетах. На значение энергии влияет выбор системы. Так, согласно системе СИ, она измеряется в джоулях (Дж). Кинетическая энергия тела характеризуется массой m, а также скоростью перемещения υ. В этом случае она составит: E_k = ((υ*υ)*m)/2.

Исходя из вышеуказанной формулы, можно сделать вывод, что кинетическую энергию определяют массой и скоростью. Иными словами, она представляет собой функцию движения тела.

Энергия в механической системе

Кинетическая энергия представляет собой энергию механической системы. Она зависит от скорости движения ее точек. Данная энергия любой материальной точки представляется такой формулой: E = 1/2mυ 2, где m – масса точки, а υ – ее скорость.

Кинетическая энергия механической системы являет собой арифметическую сумму таких же энергий всех ее точек. Ее также можно выразить следующей формулой: E_k = 1/2Mυ c2 + Ec, где υc — скорость центра масс, М – масса системы, Ec – кинетическая энергия системы при движении вокруг центра масс.

Энергия твердого тела

Кинетическая энергия тела, которое движется поступательно, определяется как и такая же энергия точки с массой, равной массе всего тела. Для расчета показателей при перемещении применяются более сложные формулы. Изменение этой энергии системы в момент ее перемещения из одного положения в другое происходит под воздействием приложенных внутренних и внешних сил. Оно равняется сумме работ Aue и A'u данных сил при этом перемещении: E2 – E1 = ∑u Aue + ∑u A'u.

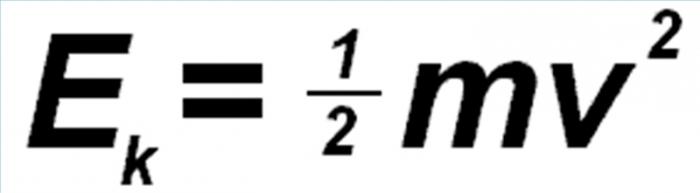
Данное равенство отражает теорему, касающуюся изменения кинетической энергии. С ее помощью решаются самые разные задачи механики. Без этой формулы невозможно решить целый ряд важнейших задач.

Кинетическая энергия при высоких скоростях

Если скорости тела близки к скорости света, кинетическую энергию материальной точки можно рассчитать по следующей формуле:

E = m0c2/√1-υ2/c2 - m0c2,

где с - скорость света в вакууме, m0 - масса точки, m0с2 - энергия точки. При маленькой скорости (υ<c), предыдущее соотношение можно выразить обычной формулой: 1/2mu2.

Энергия при вращении системы

Во время вращения тела вокруг оси каждый его элементарный объем массой (mi) описывает окружность радиусом ri. В этот момент объем имеет линейную скорость υi. Поскольку рассматривается твердое тело, угловая скорость вращения всех объемов будет одинакова: ω = υ1/r1 = υ2/r2 = … = υn/rn (1).

Кинетическая энергия вращения твердого тела представляет собой сумму всех таких же энергий его элементарных объемов: E = m1υ1 2/2 + miυi 2/2 + … + mnυn 2/2 (2).

При использовании выражения (1), получаем формулу: E = Jz ω 2/2, где Jz – это момент инерции тела вокруг оси Z.

При сравнении всех формул становится ясно, что момент инерции – это и есть мера инертности тела во время вращательного движения. Формула (2) подходит для объектов, вращающихся относительно неподвижной оси.

Плоское движение тела

Кинетическая энергия тела, движущегося вниз по плоскости, складывается из энергии вращения и поступательного движения: E = mυc2/2 + Jz ω 2/2, где m – масса движущегося тела, Jz - момент инерции тела вокруг оси, υc – скорость центра масс, ω - угловая скорость.

Изменение энергии в механической системе

Изменение значения кинетической энергии тесно связано с потенциальной. Суть этого явления можно понять благодаря закону сохранения энергии в системе. Сумма E + dP во время перемещения тела всегда будет одинаковой. Изменение значения E всегда происходит одновременно с изменением dP. Таким образом, они преобразуются, словно перетекая друг в друга. Такое явление можно встретить практически во всех механических системах.

Взаимосвязь энергий

Потенциальная и кинетическая энергии тесно связаны между собой. Их сумму можно представить как полную энергию системы. На молекулярном уровне - это внутренняя энергия тела. Она присутствует постоянно, пока существует хотя бы какое-то взаимодействие между телами и тепловое движение.

Выбор системы отсчета

Для проведения вычисления значения энергии выбирают произвольный момент (его считают начальным) и систему отсчета. Определить точную величину потенциальной энергии возможно только в зоне воздействия сил, которые не зависят от траектории движения тела при совершении работы. В физике данные силы называют консервативными. Они имеют постоянную связь с законом сохранения энергии.

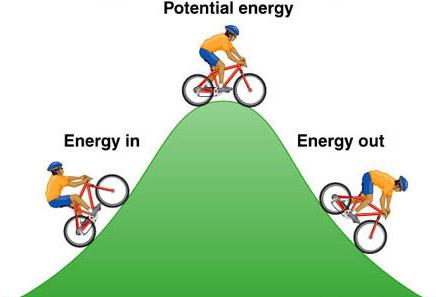
Суть разницы между потенциальной и кинетической энергией

Если внешнее воздействие минимально или сводится к нулю, изучаемая система всегда будет тяготеть к состоянию, в котором ее потенциальная энергия также будет стремиться к нулю. Например, подброшенный вверх мячик достигнет предела этой энергии в верхней точке траектории движения и в тот же момент начнет падать вниз. В это время накопленная в полете энергия преобразуется в движение (выполняемую работу). Для потенциальной энергии в любом случае существует взаимодействие как минимум двух тел (в примере с мячиком гравитация планеты оказывает на него влияние). Кинетическую энергию можно рассчитать индивидуально для любого движущегося тела.

Взаимосвязь разных энергий

Потенциальная и кинетическая энергия изменяются исключительно при взаимодействии тел, когда действующая на тела сила совершает работу, значение которой отлично от нуля. В замкнутой системе работа силы тяготения или упругости равняется изменению потенциальной энергии объектов со знаком «-»: A = - (Ep2 – Ep1).

Работа силы тяготения или упругости равняется изменению энергии: A = Ek2 – Ek1.

Из сравнения обоих равенств ясно, что изменение энергии объектов в замкнутой системе равняется изменению потенциальной энергии и противоположно ему по знаку: Ek2 – Ek1 = - (Ep2 – Ep1), или иначе: Ek1 + Ep1 = Ek2 + Ep2.

Из указанного равенства видно, что сумма этих двух энергий тел в замкнутой механической системе и взаимодействующих силами упругости и тяготения, всегда остается постоянной. Исходя из вышеизложенного, можно сделать вывод о том, что в процессе изучения механической системы следует рассматривать взаимодействие потенциальной и кинетической энергий.