Площадь трапеции: формулы и методика вычислений

Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы - непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.

Определяем трапецию

Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование "боковые стороны" или "бедра". Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.

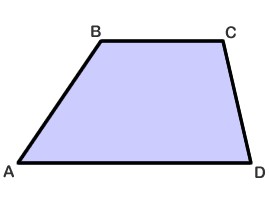
Свойства трапеции

Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком – это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:

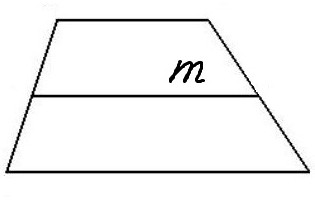
m = (a+b)/2.

Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!

У трапеции всегда можно опустить высоту на основание. Высота – это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.

Самые простые формулы площади трапеции

Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:

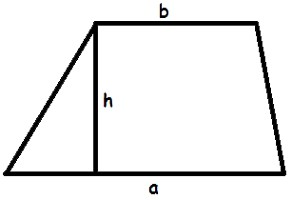
S = h*(a + b)/2.

В этой формуле a, b обозначают основания трапеции, h - высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.

Рассмотрим пример.

Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?

Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.

Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.

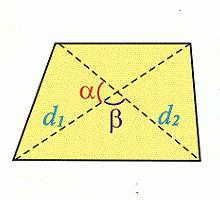
Использование диагоналей для вычислений

Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d₁ d₂) на синус угла между ними:

S = ½ d₁ d₂ sina.

Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.

Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.

Ищем площадь равнобокой трапеции

Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.

Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:

S = c*sin a*(a – c*cos a),

где с - боковое бедро, a – угол при нижнем основании.

Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции – полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d² sina.

Находим площадь прямоугольной трапеции

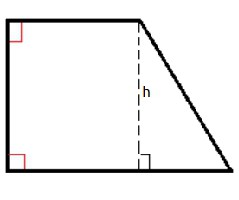
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.

Применяем смекалку

Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.

Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.

Решение

Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.

Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.

Используем формулу Пика

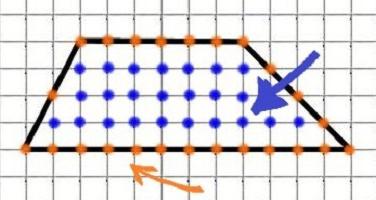
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:

S = M/2 + N – 1,

в этой формуле M – количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N – количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.

Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.

Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.