Как найти сторону треугольника - в помощь школьнику

Есть несколько способов решения этой геометрической задачи. Они описаны в статье.

При помощи сторон и углов

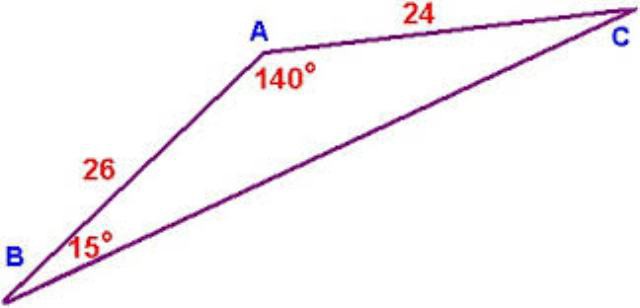
Итак, первый способ нахождения сторон треугольника - это по нескольким сторонам и углу между ними (и аналогично с углами и одной прилежащей стороной). Данный способ подойдет для старшей школы, так как здесь используются такие понятия, как синус, косинус, квадрат числа и корень. Итак, как найти сторону треугольника, который является произвольным? Для начала нарисуем эту самую фигуру. Теперь давайте обзовем элементы нашей фигуры. Стороны будут a, b и c. Угол, находящийся напротив стороны a, у нас будет "альфа", напротив b -"бета", напротив c - "гамма".

Для того чтобы найти сторону, скажем, a, необходимо вычислить квадратный корень из суммы квадрата b, c и вычесть из нее двойное произведение косинуса угла a на стороны b и c. То есть, для того, чтобы облегчить вид формулы и пояснить, как найти сторону треугольника произвольной формы, можем написать следующее: a=(b*b+c*c-2*b*c*cos"альфа")^(1/2). Будьте внимательны, ведь если угол, расположенный напротив искомой стороны, будет тупым, то косинус примет отрицательное значение. Еще одна формула нахождения сторон треугольника - по двум углам и сторонам. Сразу приведем формулу-равенство, так как для понимания наглядный вид проще, чем длинная роспись. По-прежнему нам нужно найти сторону a. Тогда, опираясь на обозначения, получим следующее: a=(b*sin"альфа")/sin"бета"=(b*sin"альфа")/sin("альфа"+"гамма")=(b*sin("бета"+"гамма"))/sin"бета". Вот таким мудреным способом можно найти неизвестную сторону произвольного треугольника.

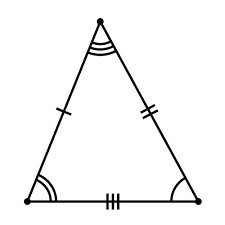
Равнобедренный треугольник

Что такое равнобедренный треугольник? Сам по себе он имеет две одинаковые стороны и так называемое основание. Стороны-близнецы обозначим буквой a, основание - b. Стало быть, раз у треугольника есть два "бедра" одной величины, то и углы на "фундаменте" тоже будут одинаковыми. Их назовем "альфа". Для того чтобы ответить, как найти сторону равнобедренного треугольника, необходимо ввести еще одну величину - угол, образованный между равными "бедрами".
Так как он располагается напротив b, то назвать его лучше всего "бета". Здесь при поиске неизвестных сторон можно пользоваться несколькими формулами. Давайте же посмотрим, какими именно. Первые две - это те, по которым можно вычислить длину стороны основания равнобедренного треугольника. Основана она на знаниях ученика о синусах и косинусах.

Итак, выглядят наши вычисления следующим образом: b=2*a*sin("бета"/2)=a*(2-2*cos"бета")^(1/2) или же b=2*a*cos"альфа". Легко все и просто. Особенно, если "набить руку" и попрактиковаться. Теперь можем взглянуть, как вычислить длину равных сторон. Здесь тоже имеется два варианта, они немного сложнее, чем предыдущие. Выглядят громоздко, но пугаться этого не стоит. Как же найти "бедра"? Будем иметь следующий вид формул: a=b/(2*sin("бета"/2))=b/(2-2*cos"бета")^(1/2) или же a=b/(2/cos"альфа"). Какую именно запись нужно использовать? Все зависит от поставленной задачи и условий. Конечно же, можно произвести проверку вычислений по всем формулам, если у вас есть абсолютно все данные. Теперь можем двигаться дальше.

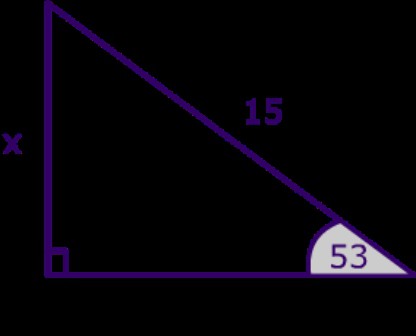
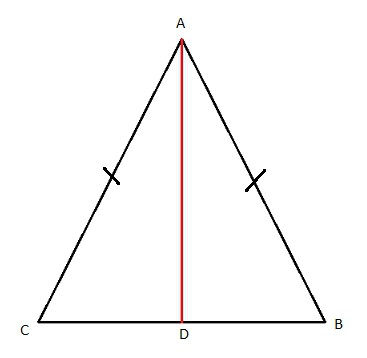
Прямоугольный треугольник

Наверное, каждый школьник, который только начал изучение геометрии, знает, что такое прямоугольный треугольник. С первого взгляда в данной фигуре нет ничего особенного, сложного и непонятного. Но вот когда "теряются" данные о той или иной стороне сего геометрического объекта, начинаются проблемы. Дело все в том, что вопрос: "Как найти сторону прямоугольного треугольника?" - затрагивает не только понятия синуса и косинуса, а еще и тангенсов углов. Таким образом, вычисления становятся намного сложнее и больше. Итак, сначала обозначим два катета нарисованного прямоугольного треугольника через a и b. Углы, лежащие напротив этих сторон, как и принято было прежде, назовем "альфа" и "бета" соответственно. Нашей гипотенузой будет служить сторона c. Угол, лежащий против него, нам не понадобится - он будет прямым. Вариантов вычислений тут несколько. Первый называется классическим. Для катета a формулы выглядит как: a=c*cos"бета"=c*sin"альфа"=b*tg"альфа".

Сторону b найдем аналогичным способом: b=c*cos"альфа"=c*sin"бета"=a*tg"бета". Тогда наша гипотенуза находится при помощи: c=a/sin"альфа"=a/cos"бета" или c=b/cos"альфа"=b/sin"бета". Второй, более простой и привычный метод нахождения сторон прямоугольного треугольника - по теореме Пифагора. Она гласит: сумма квадратов двух катетов равна квадрату гипотенузы. Значит, будем иметь следующее: a=(c*c-b*b)^(1/2), b=(c*c-a*a)^(1/2), c=(b*b+a*a)^(1/2). Вот простой и незамысловатый ответ на вопрос, как найти сторону треугольника. Не пугайтесь огромных вычислений.

Итоги

Итак, сегодня мы разобрались, как найти сторону треугольника, и выучили много новых формул. Для того чтобы лучше их запомнить, запишите их на какую-нибудь бумажку, по которой потом будет проще учить все наизусть. Не стоит пугаться "страшных" цифр и больших вычислений. Все проще, чем кажется.