Как найти площадь равнобедренного треугольника?

Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь, нужно решать задачи и примеры, чертить схемы и рисунки, доказывать теоремы.

Путь к пониманию геометрии лежит через решение задач. Отличным примером могут служить задания, в которых нужно найти площадь равнобедренного треугольника.

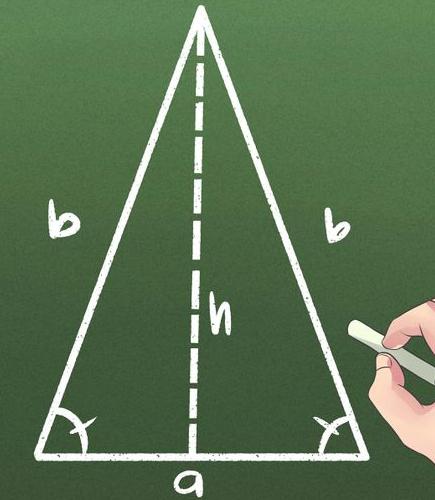
Что такое равнобедренный треугольник, и в чем его отличие от других?

Чтобы не пугаться терминов «высота», «площадь», «основания», «равнобедренного треугольника» и прочих, потребуется начать с теоретических основ.

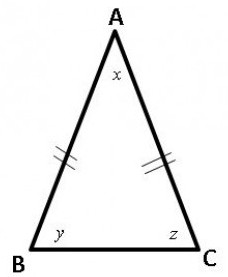
Сначала о треугольнике. Это плоская фигура, которая образована из трех точек — вершин, в свою очередь, соединенных отрезками. Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.

Существует частный случай равнобедренного треугольника — равносторонний, когда и третья сторона равна двум боковым.

Свойства фигуры

Они оказываются верными помощниками в решении задач, которые требуют найти площадь равнобедренного треугольника. Поэтому знать и помнить о них необходимо.

• Первое из них: углы равнобедренного треугольника, одна сторона которых — основание, всегда равны друг другу.
• Важным является и свойство о дополнительных построениях. Проведенные к непарной стороне высота, медиана и биссектриса совпадают.
• Эти же отрезки, проведенные из углов при основании треугольника, попарно равны. Это тоже часто облегчает поиск решения.
• Два равных угла в нем всегда имеют значение меньше чем 90º.
• И последнее: вписанная и описанная окружности строятся так, что их центры лежат на высоте к основанию треугольника, а значит медиане и биссектрисе.

Как в задаче распознать равнобедренный треугольник?

Если при решении задания встает вопрос о том, как найти площадь равнобедренного треугольника, то сначала нужно понять, что он относится к этой группе. А в этом помогут определенные признаки.

• Равны два угла или две стороны треугольника.
• Биссектриса является еще и медианой.
• Высота треугольника оказывается медианой или биссектрисой.
• Равны две высоты, медианы или биссектрисы фигуры.

Обозначения величин, принятые в рассматриваемых формулах

Для упрощения того, как находить площадь равнобедренного треугольника по формулам, введена замена его элементов на буквы.

Обозначения в формулах

Буква в формуле	Название
а	боковая сторона
в	длина основания
н	высота к основанию
А	угол при основании
В	величина угла, лежащего между боковыми сторонами
общепринятое обозначение	площадь

Внимание! Важно не путать «а» с «А» и «в» с «В». Это разные величины.

Формулы, которыми можно воспользоваться в разных задачах

Известны длины сторон, и требуется найти площадь равнобедренного треугольника.

В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:

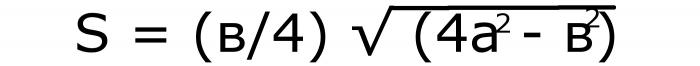
Пусть она будет записана под №1.

Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.

Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:

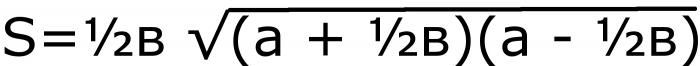
Это формула №2.

Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.

Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:

Номер этой формулы - 3.

В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.

Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:

Порядковый номер формулы — 4.

В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.

Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:

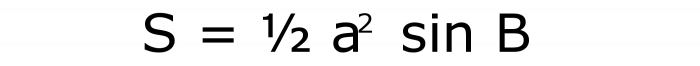
Ее номер - 5.

Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.

Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:

Номер последней формулы - 6.

Примеры задач

Первая задача: известно, что основание равнобедренного треугольника равно 10 см, а его высота - 5 см. Нужно определить его площадь.

Для ее решения логично выбрать формулу под номером 3. В ней все известно. Подставить числа и сосчитать. Получится, что площадь равна 10 * 5 / 2. То есть 25 см².

Вторая задача: в равнобедренном треугольнике даны боковая сторона и основание, которые равны соответственно 5 и 8 см. Найти его площадь.

Первый способ. По формуле №1. При возведении в квадрат основания получается число 64, а учетверенный квадрат боковой стороны — 100. После вычитания из второго первого получится 36. Из него прекрасно извлекается корень, который равен 6. Основание, поделенное на 4, равно 2. Итоговое значение определится как произведение 2 и 6, то есть 12. Это ответ: искомая площадь равна 12 см².

Второй способ. По формуле №2. Половина основания равна 4. Сумма боковой стороны и найденного числа дает 9, их же разность — 1. После умножения получается 9. Извлечение квадратного корня дает 3. И последнее действие, умножение 3 на 4, что дает те же 12 см².

Совет: как полюбить математику

Решая задачи по геометрии и определяя, как найти площадь равнобедренного треугольника, можно получить неоценимый опыт. Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.