Как найти высоту трапеции: формулы на все случаи жизни
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.
Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
В исходных данных: все стороны
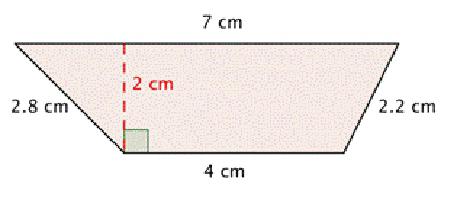
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с2 - (((а - в)2 + с2 - d2)/(2(а - в)))2). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с2 - (а - в)2/4). Номер 2.
В задаче даны: боковые стороны и углы при нижнем основании
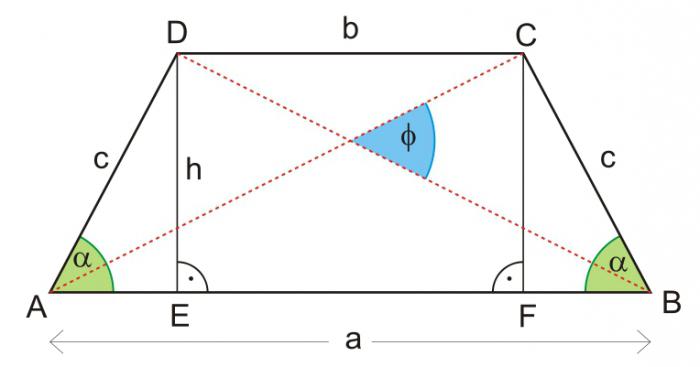
Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:
н = с * sin α= d * sin β. Номер 3.
Если фигура равнобедренная, то можно воспользоваться таким вариантом:
н = с * sin α= ((а - в) / 2) * tg α. Номер 4.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
н = (d1* d2 * sin γ) / (а + в) или н = (d1* d2 * sin δ) / (а + в). Номер 5.
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d12 * sin γ) / (а + в) или н = (d12 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1* d2 * sin γ) / 2m или н = (d1* d2 * sin δ) / 2m. Номер 5а.
н = (d12 * sin γ) / 2m или н = (d12 * sin δ) / 2m. Номер 6а.
Среди известных величин: площадь с основаниями или средней линией
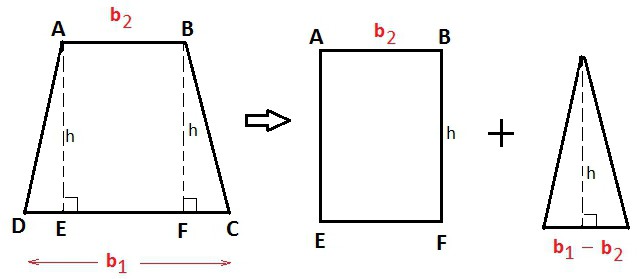
Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:
н = 2S / (а + в). Номер 7.
Она же, но с известной средней линией:
н = S / m. Номер 7а.
Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.
Задачи
№1. На определение углов при нижнем основании трапеции.
Условие. Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.
Решение. Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.
Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н1 и Н2, соответственно. Поскольку в фигуре ВСН1Н2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н1Н2 равен 6 см.
Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 - 6 нужно поделить на 2. АН1 = Н2Д = 3 (см).
Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН1 = √(52 - 32) = 4 (см).
Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН1 / АВ = 0,8.
Ответ. Искомый синус равен 0,8.
№2. На нахождение высоты трапеции по известному тангенсу.
Условие. У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.
Решение. Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН1 = Н2Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.
Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН1 / ВН1. Причем это отношение равно 11/13 (по условию). Так как АН1 известен, то можно вычислить высоту: ВН1= (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.
Ответ. Искомая высота равна 5,5 см.
№3. На вычисление высоты по известным диагоналям.
Условие. О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.
Решение. Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.
Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д1. Получилась новая трапеция, внутри которой начерчен треугольник АСД1. Он-то и нужен для дальнейшего решения задачи.
Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.
В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.
Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 √10 (см2).
Теперь нужно сосчитать высоту: н = (2 * 6 √10) / 14 = 6√10 / 7 (см).
Ответ. Высота равна 6√10 / 7 см.
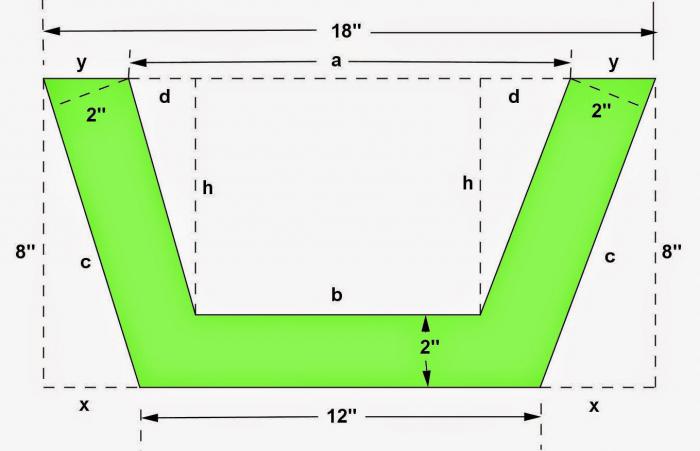
№4. Для поиска высоты по сторонам.
Условие. Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.
Решение. Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:
н = √(102 - (10 - 24)2/4) = √51 (см).
Ответ. н = √51 см.
Похожие статьи
- Все варианты того, как найти площадь трапеции
- Прямоугольная трапеция: все формулы и примеры задач
- Как находить среднюю линию треугольника? Основные свойства, определения и способы
- Прямоугольный треугольник и его свойства
- Как узнать площадь многоугольника?
- Как найти площадь равнобедренного треугольника?
- Объем конуса, его расчет
