Как формулируется и доказывается теорема косинусов?
Не все школьники, а тем более взрослые, знают, что теорема косинусов напрямую связана с теоремой Пифагора. Точнее сказать, последняя является частным случаем первой. Этот момент, а также два способа доказательства теоремы косинусов помогут стать более знающим человеком. К тому же практика в выражении величин из исходных выражений хорошо развивает логическое мышление. Длинная формула изучаемой теоремы обязательно заставит потрудиться и посовершенствоваться.
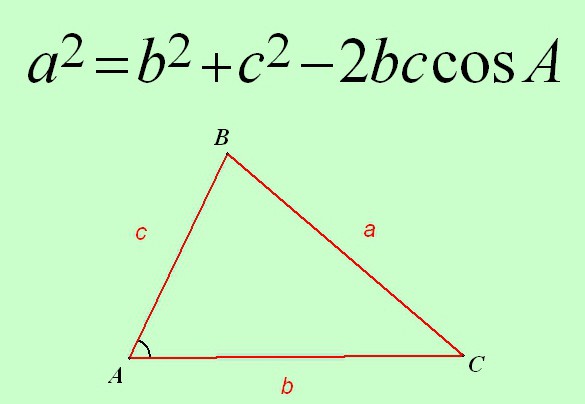
Начало разговора: введение обозначений
Эта теорема формулируется и доказывается для произвольного треугольника. Поэтому ею можно воспользоваться всегда, в любой ситуации, если даны две стороны, а в некоторых случаях три, и угол, причем необязательно между ними. Каким бы ни был вид треугольника, теорема сработает всегда.
А теперь про обозначение величин во всех выражениях. Лучше сразу договориться, чтобы потом несколько раз не пояснять. Для этого составлена следующая таблица.
| Элемент треугольника | Его обозначение |
| Неизвестная сторона | а |
| Две другие стороны | в, с |
| Угол, лежащий напротив неизвестной стороны | А |
| Углы, которые лежат против других сторон | В, С |
| Высота из вершины треугольника | н |
Формулировка и математическая запись
Итак, формулируется теорема косинусов следующим образом:
Квадрат стороны любого треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих же сторон на косинус угла, лежащего между ними.
Конечно, оно длинное, но если понять его суть, то запомнить будет просто. Можно даже представлять себе чертеж треугольника. Наглядно всегда проще запоминать.
Формула же этой теоремы будет выглядеть так:
а2 = в2 + с2 - 2 * в * с * cos А.
Немного длинно, но все логично. Если немного внимательнее посмотреть, то можно увидеть, что буквы повторяются, значит, и запомнить ее несложно.
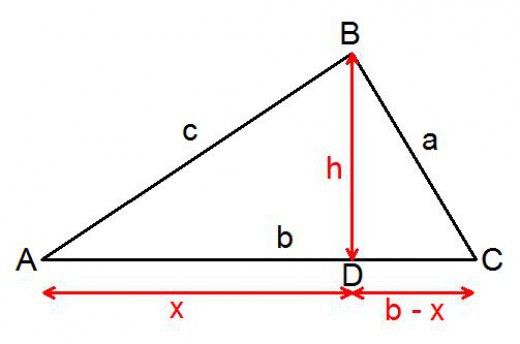
Распространенное доказательство теоремы
Поскольку она справедлива для всех треугольников, то можно выбрать для рассуждений любой из видов. Пусть это будет фигура со всеми острыми углами. Рассмотрим произвольный остроугольный треугольник, у которого угол С больше, чем угол В. Из вершины с этим большим углом нужно опустить перпендикуляр на противоположную сторону. Проведенная высота разделит треугольник на два прямоугольных. Это потребуется для доказательства.
Сторона окажется разделенной на два отрезка: х, у. Их нужно выразить через известные величины. Та часть, которая окажется в треугольнике с гипотенузой, равной в, выразится через запись:
х = в * cos А.
Другая будет равна такой разности:
у = с - в * cos А.
Теперь нужно записать теорему Пифагора для двух получившихся в результате построения прямоугольных треугольников, принимая за неизвестную величину высоту. Эти формулы будут выглядеть так:
н2 = в2 - (в * cos А)2,
н2 = а2 - (с - в * cos А)2.
В этих равенствах стоят одинаковые выражения слева. Значит, их правые части тоже будут равны. Это просто записать. Теперь нужно раскрыть скобки:
в2 - в2 * (cos А)2 = а2 - с2 + 2 с * в * cos А - в2 * (cos А )2.
Если здесь выполнить перенос и приведение подобных слагаемых, то получится начальная формула, которая записана после формулировки, то есть теорема косинусов. Доказательство закончено.
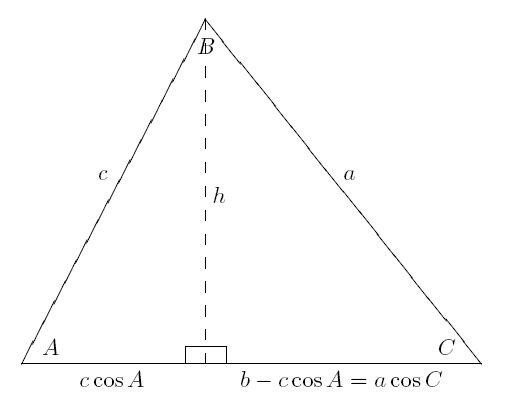
Доказательство теоремы через векторы
Оно гораздо короче предыдущего. И если знать свойства векторов, то теорема косинусов для треугольника будет доказана просто.
Если стороны а, в, с обозначить соответственно векторами ВС, АС и АВ, то справедливо равенство:
ВС = АС - АВ.
Теперь нужно выполнить некоторые действия. Первое из них — это возведение в квадрат обеих частей равенства:
ВС2 = АС2 + АВ2 - 2 АС * АВ.
Потом равенство нужно переписать в скалярном виде, учитывая то, что произведение векторов равно косинусу угла между ними на их скалярные значения:
ВС2 = АС2 + АВ2 - 2 АС * АВ * cos А.
Осталось только вернуться к старым обозначениям, и снова получится теорема косинусов:
а2 = в2 + с2 - 2 * в * с * cos А.
Формулы для других сторон и всех углов
Чтобы найти сторону, из теоремы косинусов нужно извлечь квадратный корень. Формула для квадратов одной из других сторон будет выглядеть так:
с2 = а2 + в2 - 2 * а * в * cos C.
Чтобы записать выражение для квадрата стороны в, нужно в предыдущем равенстве заменить с на в, и наоборот, и под косинусом поставить угол В.
Из основной формулы теоремы можно выразить значение косинуса угла А:
cos А = (в2 + с2 - а2) / (2 в * с).
Аналогично выводятся формулы для других углов. Это хорошая практика, поэтому можно попробовать написать их самостоятельно.
Естественно, что запоминать эти формулы нет необходимости. Достаточно понимания теоремы и умения вывести эти выражения из ее основной записи.
Исходная формула теоремы дает возможность найти сторону, если угол лежит не между двумя известными. К примеру, нужно найти в, когда даны величины: а, с, А. Или неизвестна с, зато есть значения а, в, А.
В этой ситуации нужно перенести все слагаемые формулы в левую сторону. Получится такое равенство:
с2 - 2 * в * с * cos А + в2 - а2 = 0.
Перепишем его немного в другом виде:
с2 - (2 * в * cos А) * с + (в2 - а2) = 0.
Можно легко увидеть квадратное уравнение. В нем неизвестная величина - с, а все остальные даны. Поэтому его достаточно решить с помощью дискриминанта. Так будет найдена неизвестная сторона.
Аналогично получается формула для второй стороны:
в2 - (2 * с * cos А) * в + (с2 - а2) = 0.
Из других выражений такие формулы тоже легко получить самостоятельно.
Как без вычисления косинуса узнать вид угла?
Если внимательно посмотреть на формулу косинуса угла, выведенную ранее, то можно заметить следующее:
- знаменатель дроби - всегда положительное число, потому что в нем стоит произведение сторон, которые не могут быть отрицательными;
- значение угла будет зависеть от знака числителя.
Угол А будет:
- острым в ситуации, когда числитель больше нуля;
- тупым, если это выражение отрицательное;
- прямым при его равенстве нулю.
Кстати, последняя ситуация обращает теорему косинусов в теорему Пифагора. Потому что для угла в 90º его косинус равен нулю, и последнее слагаемое исчезает.
Первая задача
Условие
Тупой угол некоторого произвольного треугольника равен 120º. О сторонах, которыми он ограничен, известно, что одна из них больше другой на 8 см. Известна длина третьей стороны, это 28 см. Требуется найти периметр треугольника.
Решение
Сначала нужно обозначить одну из сторон буквой «х». В таком случае другая будет равна (х + 8). Поскольку есть выражения для всех трех сторон, можно воспользоваться формулой, которую дает теорема косинусов:
282 = (х + 8)2 + х2 - 2 * (х + 8) * х * cos 120º.
В таблицах для косинусов нужно найти значение, соответствующее 120 градусам. Это будет число 0,5 со знаком минус. Теперь полагается раскрыть скобки, соблюдая все правила, и привести подобные слагаемые:
784 = х2 + 16х + 64 + х2 - 2х * (-0,5) * (х + 8);
784 = 2х2 + 16х + 64 + х2 + 8х;
3х2 + 24х - 720 = 0.
Это квадратное уравнение решается через нахождение дискриминанта, который будет равен:
Д = 242 - 4 * 3 * (- 720) = 9216.
Поскольку его значение больше нуля, то уравнение имеет два ответа-корня.
х1 = ((-24) + √(9216)) / (2 * 3) = 12;
х2 = ((-24) - √(9216)) / (2 * 3) = -20.
Последний корень не может быть ответом задачи, потому что сторона обязательно должна быть положительной.
Итак, две стороны известны. Легко найти третью: 12 + 8 = 20 (см). Теперь можно ответить на вопрос задачи. Периметр треугольника определяется как сумма всех сторон:
24 + 12 + 20 = 60 (см).
Ответ: периметр равен 60 сантиметрам.

Задача №2
Условие
В треугольнике известны: с, равное 2 см; а, которое составляет 10 см; угол С величиной 120º. Требуется найти сторону в.
Решение
Для начала нужно воспользоваться теоремой косинусов и вывести из нее формулу квадратного уравнения, в которой неизвестной будет величина в:
с2 = а2 + в2 - 2 * а * в * cos C
и
в2 - (2 * а * cos С) * в + (а2 - с2) = 0.
В нее нужно подставить все известные в условии величины:
в2 - (2 * 10 * cos 120º) * в + (102 - 22) = 0.
Теперь нужно сосчитать то, что возможно, чтобы упростить выражение:
в2 - (20 * (-1/2)) * в + (100 - 4) = 0
или
в2 + 10 * в - 96 = 0.
Это стандартное квадратное уравнение, которое нужно решить через нахождение дискриминанта:
Д = (10)2 - 4 * 1 * (-96) = 484.
По формулам нужно произвести вычисления для неизвестной стороны:
в1 = (- 10 + 22) / 2 = 6 (см);
в2 = (- 10 - 22) / 2 = - 16 — этот корень не удовлетворяет решению задачи, потому что сторона не может быть отрицательной.
Ответ: неизвестная сторона равна 6 см.
Третья задача
Условие
В некотором треугольнике даны стороны: а, в, с, которые соответственно равны 6 см, 10 см и 8 см. Требуется вычислить угол А.
Решение
Снова нужно воспользоваться теоремой косинусов. Используется та ее запись, в которой есть косинус угла А, поскольку именно его необходимо вычислить. Вот написана сразу формула для косинуса неизвестного угла:
cos А = (в2 + с2 - а2) / (2 в * с).
Осталось подставить значения сторон и выполнить все вычисления:
cos А = (102 + 82 - 62) / (2 * 8 * 10).
После возведения всех слагаемых в квадрат и умножения чисел из знаменателя:
cos А = (100 + 64 - 36) / (160).
После сложения и деления получается:
cos А = 128 / 160 = 0,8.
Теперь нужно воспользоваться таблицей Брадиса, чтобы узнать, чему равен угол А. Ближайшее значение угла для этого косинуса составляет 36º54´.
Ответ: значение угла А равно 36º54´.
Похожие статьи
- Находим периметр треугольника различными способами
- Правила, по которым происходит сложение векторов
- Как вычислить углы между векторами?
- Периметр квадрата и прямоугольника. Способы определения и примеры решения.
- Площадь трапеции: формулы и методика вычислений
- Простая задача: как найти периметр?
- Как найти сторону треугольника - в помощь школьнику
