Дифракция Френеля на круглом отверстии и диске

Дифракция света проявляется в огибании световыми волнами небольших препятствий, при этом наблюдаются отклонения от законов геометрической оптики. Это также относится и к световым волнам, проходящим через отверстие, например, в объективе фотокамеры или через зрачок глаза. Есть дифракция Френеля и Фраунгофера. Различия состоят в величине расстояния между источником света, препятствием и экраном, на котором наблюдается картина этого явления.

Место дифракции в общем ряду оптических явлений

Прохождение световых (и вообще электромагнитных) волн через различные неоднородные среды сопровождается явлениями их отражения, дифракции и преломления. Когда волна достигает границы двух сред, она разделяется на отраженную, остающуюся в исходной среде, но с изменением направления распространения, и преломленную, которая проходит через границу сред, но также с изменением направления. Дифракция Френеля — это процесс изменения в направлении световой волны при встрече на своем пути не границы двух сред, а некоторого непрозрачного препятствия с отверстием (или без него, но небольших размеров) в той же среде. Степень дифракции увеличивается с ростом длины световой волны.

Открытие явления

Наверное, первым, кто наблюдал дифракцию, был Франческо Мария Гримальди (2 апреля 1618 г. - 28 декабря 1663 г.), итальянский священник-иезуит и одновременно математик и физик, преподававший в иезуитском колледже в Болонье. Вторую половину своей жизни он посвятил изучению астрономии и оптики.

Знаменитым сделала Гримальди его работа под названием "Физическая наука о свете, цветах и радуге", которая была опубликована в Болонье в 1665 году. Большая ее часть состоит из утомительного обсуждения природы света с теологических позиций и сегодня не представляет интереса. Однако, кроме этого, в книге содержатся учетные записи многочисленных экспериментов, связанных с дифракцией лучей света.

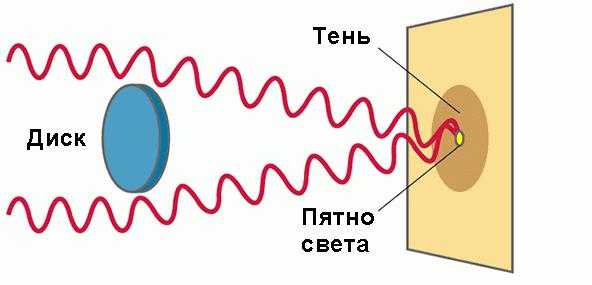
Исходя из повседневного опыта, люди еще в древности сделали вывод, что лучи света распространяются по прямым линиям. Ведь предмет, находящийся между, например, пламенем свечи и стеной, отбрасывает тень с резкой границей, как если бы прямые лучи света обрывались на непрозрачной преграде.

Однако результаты опытов Гримальди противоречили этим устоявшимся за тысячелетия представлениям. Оказывается, если освещать разные предметы через преграду с маленьким отверстием, то тени от них будут вовсе не такими, как при отсутствии преграды. Получалось, что свет способен менять направление распространения и огибать небольшие препятствия.

Как была обнаружена дифракция Френеля на круглом отверстии

Гримальди, пропустив свет солнца в темную комнату через небольшое отверстие (апертуру), заметил, что ширина тени тонких объектов вроде иглы и волоса на экране оказывается значительно большей (как видно на фото ниже), чем это было бы, если бы лучи света проходили по прямым линиям.

Он отметил также, что круг света, формируемый на экране лучами, проходящими через очень небольшое отверстие в пластине свинца, был явно больше, чем это было бы, если бы эти лучи падали на экран прямолинейно. Гримальди пришел к выводу, что они изменяют свое направление при прохождении вблизи краев отверстия.

В его опытах, проводившихся внутри одной комнаты, свет в которую попадал через отверстия в ставнях, расстояние между препятствием для световых волн (пластина с круглым отверстием) и экраном было малым. Этим условиям соответствует и такое явление, как дифракция Френеля. Анализируя ее, нельзя пренебрегать кривизной фронта как исходной падающей на препятствие волны, так и вторичных волн. Именно они дают на экране дифракционное изображение препятствия с отверстием, как показано на фото ниже.

Что происходит, если свет падает на небольшое непрозрачное препятствие

Гримальди обнаружил также, что тень небольшого тела (неправильной формы) была окружена тремя цветными полосами или лентами, которые становились более узкими по мере удаления от центра тени. Если исходный поток света был более сильным, он воспроизводил аналогичные цветные полосы и в зоне самой тени: там оказывались две или более таких полос, причем их число увеличивалось пропорционально расстоянию между тенью и освещаемым телом.

И в этом случае Гримальди удалось наблюдать явление, которое позже было названо "дифракция Френеля", в результате которого на экране получалась дифракционная картина препятствия. Аналитически рассчитать ее очень трудно. Впрочем, имеются методы, которые позволяют в некоторых частных случаях существенно упростить этот расчет.

И еще одно замечание об опытах Гримальди. Если бы он использовал в них в качестве экрана круглый диск (например, блюдце), то, возможно, ему удалось бы на полтора столетия раньше, чем это случилось в действительности, наблюдать такое явление, как дифракция Френеля на круглом диске. Но история вообще и история науки в частности не знают сослагательного наклонения. Поэтому данный опыт был выполнен только в начале 19 в. (см. ниже).

Первое наблюдение интерференции

Пропустив солнечные лучи в комнату через несколько маленьких круглых отверстий, Гримальди получил следы перекрывающихся друг другом конусов света на экране. Как и следовало ожидать, в тех областях, на которые падали лучи от двух отверстий, экран был освещен сильнее, чем это было бы от одного конуса света; но исследователь был удивлен, обнаружив, что те части суммарной тени, в которых конусы света наложены друг на друга, оказались темнее, чем соответствующие части, в которых не было никакого наложения (рисунок ниже).

Таким образом, впервые было зафиксировано, что освещенное тело может стать темнее, если добавить свет к тому, который оно уже получает. Сейчас мы знаем, что причиной этому является интерференция, т. е. взаимное усиление или ослабление световых волн. Она же проявляется и в таком явлении, как дифракция Френеля. Многие современные ученые даже принципиально не делают различий между этими понятиями, сводя все дифракционные проявления к интерференционным, как это сделал, например, Р. Фейнман в 3-м томе своих «Фейнмановских лекций по физике».

От Гримальди до Гюйгенса и Ньютона

Первую попытку объяснить причину отклонения света от прямолинейного распространения предпринял знаменитый английский ученый Р. Гук. Он предположил, что свет – это волновые колебания мирового эфира, под которым тогда понималась всепроникающая субстанция, заполняющая все пространство. В идее Гука уже была заложена основа для будущего правильного объяснения того, что такое дифракция Френеля и все оптические явления. Однако он не смог создать соответствующую количественную теорию.

Следующий шаг был сделан Христианом Гюйгесом, который сформулировал свой знаменитый принцип в 1690 г. Согласно ему, видимый свет есть совокупность распространяющихся от источника во все стороны сферических волн в эфире. При этом источником этих волн могут быть не только частицы эфира, возбужденные непосредственно источником света (например, пламенем свечи), но и любые другие его частицы в точках пространства, которые проходит свет при распространении. Результирующая видимая волна находится в любой момент времени как огибающая все вторичные волны. Последние же вполне могут распространяться и за границы препятствий на пути света, что хорошо накладывается на наблюдаемые при дифракции картины их теней. Поэтому, согласно этой теории, никакого огибания светом препятствий попросту нет – от новых (вторичных) источников он распространяется за препятствия.

Однако, согласно принципу Гюйгенса, вообще невозможны узкие световые лучи – их края сразу же должны расползаться во все стороны. Тем не менее, их можно видеть невооруженным глазом, как это было в опытах Гримальди. Возникало противоречие между теорией и практикой.

Преодолеть его попытался И. Ньютон в своей корпускулярной теории света, которая также давала объяснения всем оптическим явлениям, включая и такое, как дифракция света Френеля. Однако основной постулат Ньютона о том, что свет - это не волна в эфире, а поток тел (корпускул), породил другие противоречия. Так, было неясно, почему не влияют друг на друга пересекающиеся пучки света, ведь корпускулы должны были бы сталкиваться друг с другом. Но авторитет Ньютона был настолько высок, что волновая теория света была забыта более чем на сто лет.

Возвращение световых волн

В 1880 г. английский физик Т. Юнг предложил вернуться к волновой теории света, дополненной понятием об интерференции световых волн. Оно означает, что при наложении друг на друга когерентных (с одинаковыми частотами) волн возможно устойчивое во времени усиление интенсивности света в одних точках поля и ослабление в других в зависимости от соотношения фаз складываемых световых волн.

Понятием интерференции воспользовался французский физик О. Френель, чтобы дополнить им принцип Гюйгенса. Согласно его варианту, все вторичные сферические волны являются когерентными и интерферируют при наложении. Какой же физический механизм имеет дифракция Гюйгенса-Френеля?

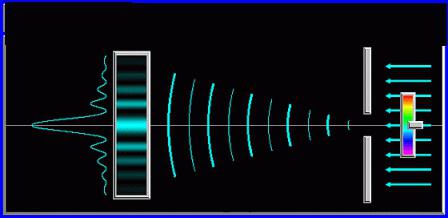
Пропускаем свет через круглое отверстие

Когда световая волна распространяется через отверстие, соотношение между его диаметром и длиной волны падающего луча определяет поведение света. Как показано на левой части рисунка ниже, когда длина волны значительно меньше, чем диаметр отверстия, она просто проходит вперед по прямой линии, как будто препятствия вообще нет.

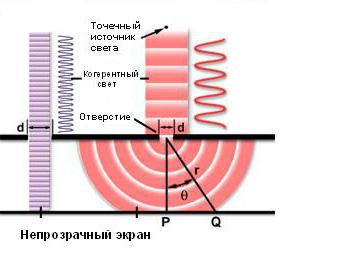
На правой стороне рисунка, однако, показана другая ситуация. В этом случае длина волны света, прошедшего от точечного источника, превышает диаметр проема, и возникает дифракция Френеля на отверстии. При анализе этого явления отверстие считают отсутствующим, а вместо него помещают совокупность фиктивных вторичных источников света, которые возбуждают те самые вторичные сферические волны, о которых уже упоминалось выше. Они распространяются в направлении экрана и достигают разных его точек с разными фазами, интерферируя друг с другом, т. е. усиливаясь или ослабляясь в каждой такой точке. Поскольку вся система обладает осевой симметрией, то падающий цилиндрический пучок света превращается в конический, а на экране наблюдается также осесимметричная дифракционная картина из чередующихся ярких и темных колец, называемых также максимумами и минимумами освещенности соответственно. В точке P, находящейся на оси отверстия, будет яркое пятно – основной максимум, а первый из вторичных максимумов освещенности возникнет в точке Q. Интенсивность вторичных максимумов уменьшается по мере увеличения их расстояния от центра дифракционной картины. Соотношение между размером отверстия и степенью дифракции определяется следующим уравнением:

sinθ = λ/d, где

• θ - угол между направлением на центр дифракционной картины и направлением на ее первый минимум,
• λ – длина световой волны.

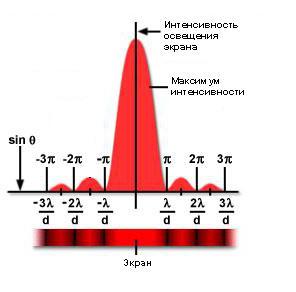
Рисунок ниже показывает, как изменяется интенсивность освещенности экрана в зависимости от углового расстояния от центра. Обратите внимание, что минимумы, находящиеся между вторичными максимумами, расположены в точках, кратных величине ∏.

Аналитический расчет картины такого явления, как дифракция Френеля на отверстии и диске, существенно упрощается вследствие осевой симметрии, о чем будет дополнительно сказано ниже.

Круглый диск на пути пучка света

Если следовать теории Френеля, то при помещении на пути пучка света круглого непрозрачного диска все точки на его краях становятся источниками когерентных вторичных сферических волн. Расстояния между этими точками и точкой пересечения оси диска с перпендикулярным ей непрозрачным экраном одинаковы. Поэтому волны от всех точек на краю диска должны пересечься в одно время и в одной фазе, т. е. они должны сложиться и значительно усилить друг друга. Получается, что в центре круглой тени от диска должно наблюдаться яркое освещенное пятно, как на рисунке ниже.

На это обстоятельство впервые обратил внимание французский физик С. Пуассон, бывший противником теории Френеля. Он считал, что отмеченное им обстоятельство доказывает ее несостоятельность. Каково же было его удивление, когда Френель совместно с Араго проделал соответствующий опыт и получил в центре тени от диска именно такое пятно! На рисунке ниже схематически показан этот опыт.

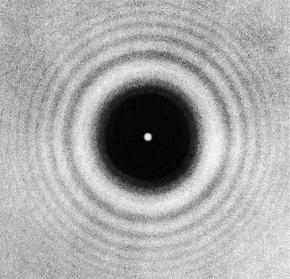
Так проявляет себя дифракция Френеля на диске. Яркое же пятно в центре его тени получило наименование пятна Пуассона. Если диск небольшой, то интенсивность света в центре его дифракционного изображения практически такая же, как и при его (диска) отсутствии.

Как рассчитывать картины дифракции

В общем случае расчет интерференции вторичных волн для получения дифракционной картины является сложным. Но в осесимметричных случаях он может быть упрощен, так что становится несложной и вся картина такого явления, как дифракция. Метод зон Френеля позволяет наглядно геометрическим способом разбить фронт сферической волны на кольцевые участки.

Амплитуды и относительные фазы всех зон принимаются во внимание для расчета распределения интенсивности. Таким образом, для определения дифракционной картины применяется достаточно сложная математическая обработка. Но при анализе такого явления, как дифракция Френеля на круглом отверстии и диске, она существенно упрощается.

На рисунке ниже S является точечным источником света.

S излучает сферическую световую волну длиной λ в направлении слева направо. Пусть радиус ее фронта в момент времени t равен R. Эффект этого волнового фронта в точке Р определяется путем его разделения на кольцевые зоны. Расстояния от краев двух последовательных зон до точки Р отличаются на λ/2. Кольцевые зоны, обладающие этим свойством, называются зонами Френеля. Расстояние от нулевой зоны до точки Р равно b₀.

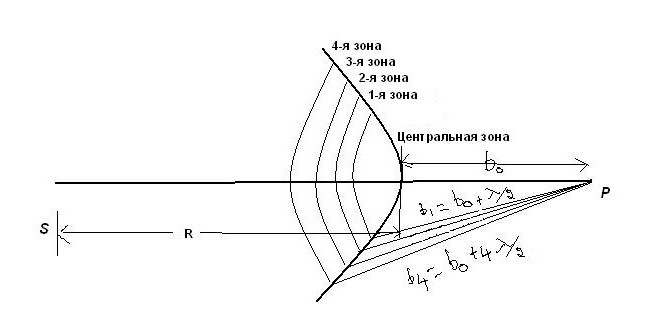
Первая зона находится на расстоянии b₁ = b₀ + λ/2; вторая: b₂ = b₀ + 2λ/2; третья: b₃ = b₀ + 3λ /2; i-я зона: b_i = b₀ + iλ /2.

Последовательно расположенные края двух соседних зон находятся в сходственных точках. Если в них возбуждаются вторичные сферические волны, то они приходят в точку наблюдения Р с разностью фаз в 180° и взаимно ослабляют друг друга при наложении (но не уничтожают).

Дифракция Френеля на круглом отверстии и диске - картина с осевой симметрией. Поэтому применение этого метода позволяет существенно упростить построение дифракционной картины при прохождении светом таких препятствий.

Как работают кольцевые зоны Френеля на круглом отверстии

Рассмотрим снова случай, когда на круглом отверстии происходит дифракция света. Зоны Френеля, на которые может быть разбит волновой фронт, укладывающиеся в отверстии данного диаметра при определенной длине волны λ и расстоянии от фронта до экрана b₀, могут оказаться в количестве, выраженном нечетным или четным числом. Как уже было отмечено выше, вторичные волны от двух соседних зон в каждой точке экрана ослабляют, хотя и не уничтожают друг друга. Поэтому, если для центра дифракционной картины число зон Френеля, укладывающихся в отверстии, нечетно (2k+1), то амплитуда освещенности в центре картины будет складываться из суммы остатка действия первой (центральной) зоны и ничем не скомпенсированного действия (2k+1)-й зоны, которые будут усиливать друг друга. Дифракционная картина для этого случая показана на рисунке ниже.

Если же число зон Френеля, укладывающихся в отверстии, будет четным, то влияние всех зон в центре картины будет взаимно попарно скомпенсировано, и в нем появится темное пятно.