Теорема Виета: примеры ее использования при работе с квадратными уравнениями

При изучении способов решения уравнений второго порядка в школьном курсе алгебры, рассматривают свойства полученных корней. Они в настоящее время известны под названием теоремы Виета. Примеры использования ее приводятся в данной статье.

Квадратное уравнение

Уравнение второго порядка представляет собой равенство, которое показано на фото ниже.

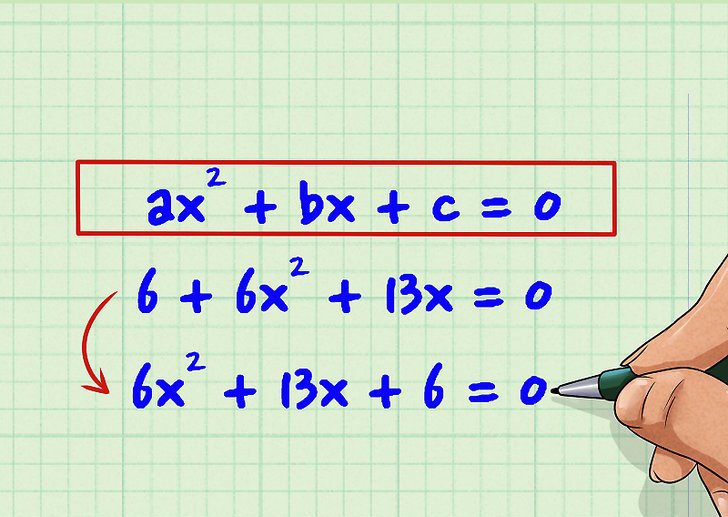
Здесь символы a, b, c являются некоторыми числами, носящими название коэффициентов рассматриваемого уравнения. Чтобы решить равенство, необходимо найти такие значения x, которые делают его истинным.

Заметим, что поскольку максимальное значение степени, в которую возводится икс, равно двум, тогда число корней в общем случае также равно двум.

Для решения этого типа равенств существует несколько способов. В данной статье рассмотрим один из них, который предполагает использование так называемой теоремы Виета.

Формулировка теоремы Виета

В конце XVI известный математик Франсуа Виет (француз) заметил, анализируя свойства корней различных квадратных уравнений, что определенные их комбинации удовлетворяют конкретным соотношениям. В частности, этими комбинациями является их произведение и сумма.

Теорема Виета устанавливает следующее: корни квадратного уравнения при их сумме дают отношение коэффициентов линейного к квадратичному взятое с обратным знаком, а при их произведении приводят к отношению свободного члена к квадратичному коэффициенту.

Если общий вид уравнения записан так, как это представлено на фото в предыдущем разделе статьи, тогда математически эту теорему можно записать в виде двух равенств:

• r₂ + r₁ = -b / a;
• r₁ х r₂ = c / a.

Где r₁, r₂ - это значение корней рассматриваемого уравнения.

Приведенные два равенства можно использовать для решения ряда самых разных математических задач. Использование теоремы Виета в примерах с решением приведены в следующих разделах статьи.

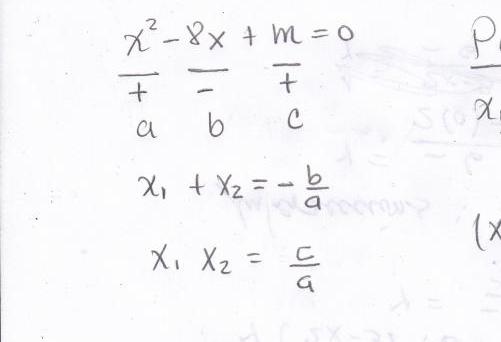
Задача №1: восстановите уравнение

Приведем следующую задачу на использование теоремы Виета. Пример уравнения дан следующий: -3,4 * x - 3 * s * x² + k = 0. Необходимо найти значения s и k, зная, что решениями этого уравнения являются два числа: -1,2 и 4.

Для начала необходимо определиться со значением коэффициентов в этом выражении. Из него следует, что a = -3 * s, b = -3,4 и c = k.

Теперь можно использовать теорему Виета. Для суммы корней мы получим следующее равенство: -1,2 + 4=-(-3,4) / (-3 * s), откуда получаем, что s = -0,40476 (для вычисления этого выражения рекомендуется воспользоваться калькулятором). То есть a = -3*s = 1,21429. Для произведения корней имеем:

(-1,2) * 4 = k / 1,21429, откуда k = -5.82859.

Восстановленное уравнение будет соответствовать виду: -3,4 * x + 1,21429 * x² - 5,82859=0. Чтобы проверить, правильно ли решена задача, и не допущена ли ошибка при ее решении, необходимо подставить известные значения корней в восстановленное выражение. Получаем: -3,4 * (-1,2) + 1,21429 * (-1,2)² - 5,82859 = 0,00001 ≈ 0 и -3,4 * (4) + 1,21429 * (4)² - 5,82859 = 0,00005 ≈ 0.

Как видим, полученные равенства действительно выполняются. Небольшая ошибка связана с тем, что при восстановлении уравнения мы округляли полученные цифры до 5 знаков после запятой.

Задача №2: найдите корни уравнения

Решение квадратных уравнений теоремой Виета (пример см. ниже) возможно осуществить не во всех случаях. То есть этот метод не является универсальным, поскольку если коэффициенты уравнения окажутся "неудобными", тогда его использовать не получится.

Универсальными способами решения этого типа выражения являются использование дискриминанта или дополнение до полного квадрата. Тем не менее, важность теоремы Виета в этом случае заключается в том, что она позволяет догадаться о неизвестных корнях, не осуществляя при этом сложных математических выкладок.

Например, дано выражение следующее: -x² + 2 * x + 3 = 0. Следует воспользоваться Виета теоремой, чтобы найти решения этого равенства. Пусть его корнями являются числа r₁ и r₂. Тогда можно записать следующую систему уравнений:

r₁ + r₂ = -2 /(-1) = 2;

r₁*r₂ = 3 / (-1) = -3.

Теперь необходимо догадаться, сумма каких чисел равна двум, а их произведение будет -3. Очевидно, что таковыми являются числа 3 и -1. Они и будут корнями названного уравнения.

Если немного углубиться в тему, то следует отметить, что любое уравнение второго порядка, которое легко представляется в виде произведения двух множителей, может быть решено с помощью обсуждаемой теоремы. Действительно, в данном случае можно записать (3-x) *(x+1), если раскрыть скобки, то мы получим исходное выражение.

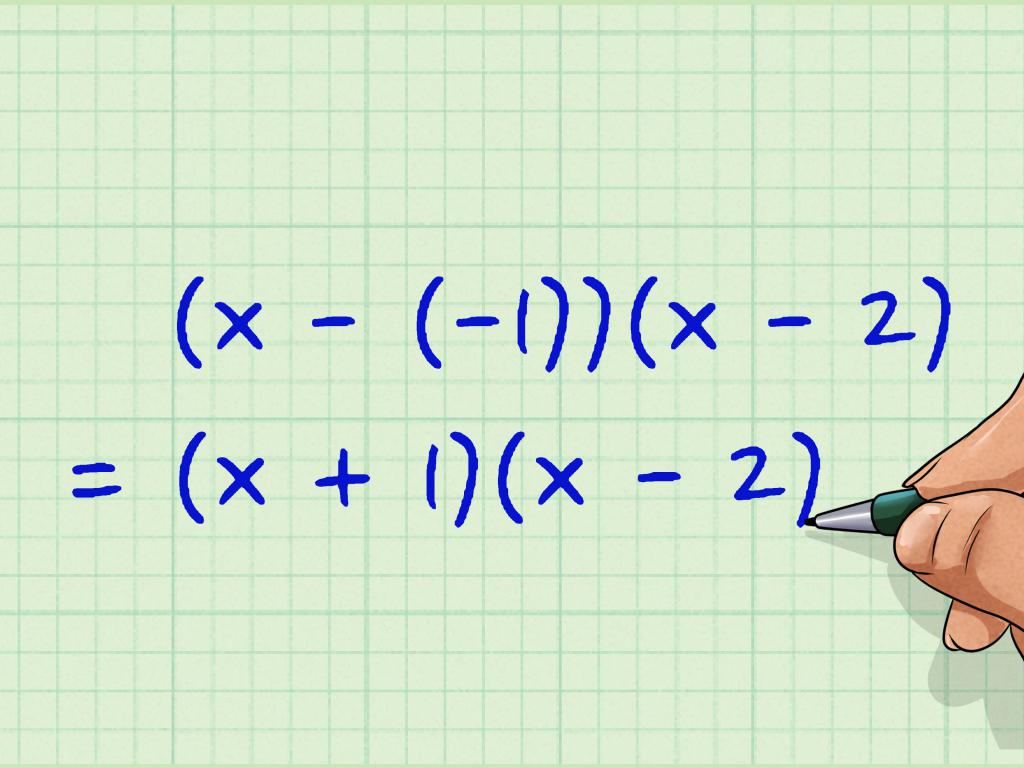
Задача №3: сумма квадратов

Приведем еще один пример теоремы Виета с решением. Дано уравнение:

6 * x² - 13 * x + 11 = 0. Необходимо найти сумму квадратов его двух корней, то есть (r₁)² + (r₂)².

Конечно, можно решить сначала это уравнение одним из способов, а затем ответить на вопрос задачи. Однако, если вспомнить про теорему Виета и про свойство квадрата суммы, то в этом нет никакой необходимости.

Следует вспомнить, как вычисляется сумма двух чисел, возведенная в квадрат. Тогда получаем, что для нахождения неизвестной суммы квадратов, необходимо вычислить значение выражения (r₁ + r₂)² - 2 * r₁ * r₂. Воспользуемся обоими равенствами рассматриваемой теоремы, получим: (13/6)² - 2 * 11 / 6 = 1,02(7) (7 в периоде).

Таким образом, применяя теорему Виета, мы сэкономили время на решение уравнения. В общем случае свойства корней можно использовать для любых задач, которые предполагают вычисление их различных комбинаций.