Что такое момент инерции: формулы для стержня и колеса

Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения. Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.

Вращение и момент инерции

Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:

L = r*m*v

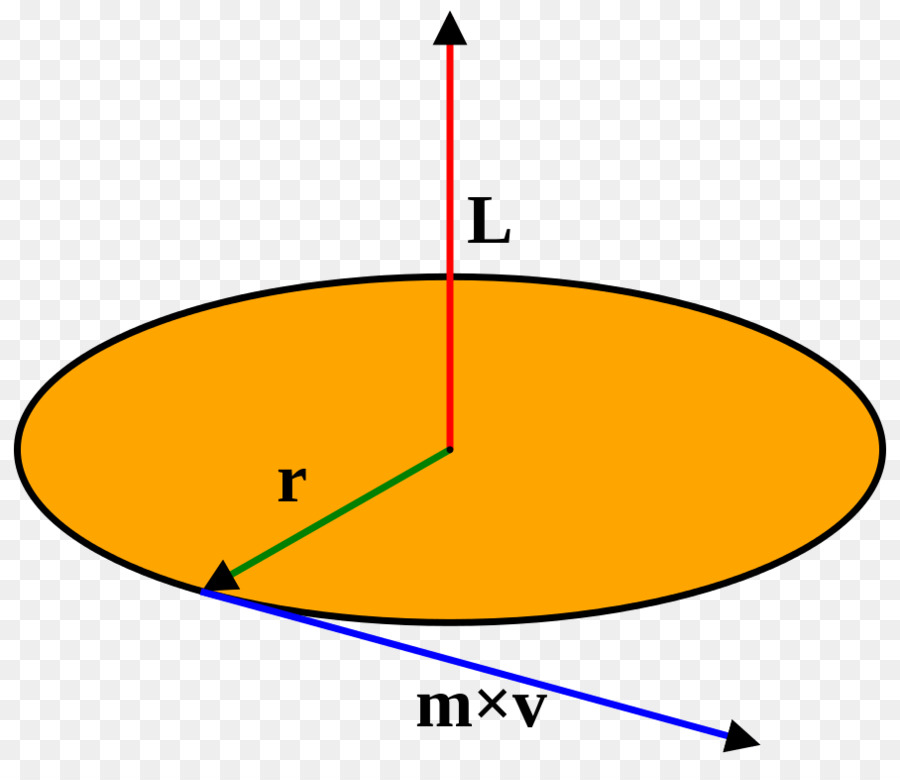
Здесь r - дистанция до оси материальной точки, m - ее масса, v - линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:

L = r²*m*ω, где ω = v/r

Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r²*m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м².

Общее выражение для момента инерции

Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:

I = ∫_m(r²*dm)

Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.

Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.

Физический смысл величины I

Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.

Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик - тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить. Примером для этого случая является алюминиевый обод велосипедного колеса.

Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.

Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.

Момент инерции относительно оси вращения, пересекающей центр масс стержня

Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.

Выпишем общую формулу для инерции момента стержня относительно оси, имеем:

I = ∫_m(r²*dm)

Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси. В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:

dm = ρ*S*dr

Здесь ρ - плотность материала, S - поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:

I = ρ*S*∫^+l/2_-l/2(r²*dr)

Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:

I = ρ*S*(r³/3)|^+l/2_-l/2 = m*l²/12, где m = ρ*S*l

Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.

Величина I для стержня с осью вращения на конце объекта

Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:

I = ρ*S*∫^l₀(r²*dr)

Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:

I = m*l²/3

Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.

Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.

Значение I для колеса со спицами

Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины. Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица - это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.

Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.

Складывая моменты инерции всех элементов, получаем:

I = n*m_c*r²/3 + m_o*r²

Здесь m_c и m_o - массы спицы и обода, соответственно, n - число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:

I =m_o*r², если n*m_c<<m_o

Знание величины I для колеса является важным при расчете скорости угловой и момента импульса вращения колес любого транспортного средства (автомобиля, велосипеда).