Поверхность призмы. Площадь основания и боковой поверхности. Площадь основания треугольной призмы

В пространственной геометрии при решении задач с призмами часто возникает проблема с расчетом площади сторон или граней, которые образуют эти объемные фигуры. Данная статья посвящена вопросу определения площади основания призмы и ее боковой поверхности.

Фигура призма

Перед тем как переходить к рассмотрению формул для площади основания и поверхности призмы того или иного вида, следует разобраться, о какой фигуре идет речь.

Призма в геометрии представляет собой пространственную фигуру, состоящую из двух параллельных многоугольников, которые равны между собой, и нескольких четырехугольников или параллелограммов. Количество последних всегда равно числу вершин одного многоугольника. Например, если фигура образована двумя параллельными n-угольниками, тогда количество параллелограммов будет равно n.

Соединяющие n-угольники параллелограммы называются боковыми сторонами призмы, а их суммарная площадь - это площадь боковой поверхности фигуры. Сами же n-угольники называются основаниями.

Выше рисунок демонстрирует пример призмы, изготовленной из бумаги. Желтый прямоугольник является ее верхним основанием. На втором таком же основании фигура стоит. Красный и зеленый прямоугольники - это боковые грани.

Какие призмы бывают?

Существует несколько типов призм. Все они отличаются друг от друга всего двумя параметрами:

• видом n-угольника, образующего основания;
• углом между n-угольником и боковыми гранями.

Например, если основания являются треугольниками, тогда и призма называется треугольной, если четырехугольниками, как на предыдущем рисунке, тогда фигура называется четырехугольной призмой, и так далее. Кроме этого, n-угольник может быть выпуклым или вогнутым, тогда к названию призмы тоже добавляется это свойство.

Угол между боковыми гранями и основанием может быть либо прямой, либо острый или тупой. В первом случае говорят о прямоугольной призме, во втором - о наклонной или косоугольной.

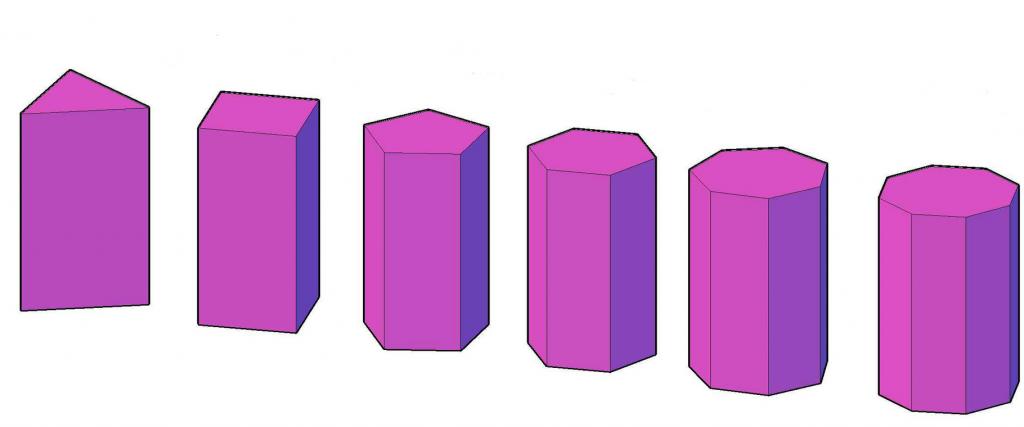
В особый тип фигур выделяют правильные призмы. Они обладают самой высокой симметрией среди остальных призм. Правильной она будет только в том случае, если является прямоугольной и ее основание - это правильный n-угольник. Рисунок ниже демонстрирует набор правильных призм, у которых число сторон n-угольника изменяется от трех до восьми.

Поверхность призмы

Под поверхностью рассматриваемой фигуры произвольного типа понимают совокупность всех точек, которые принадлежат граням призмы. Поверхность призмы удобно изучать, рассматривая ее развертку. Ниже дан пример такой развертки для треугольной призмы.

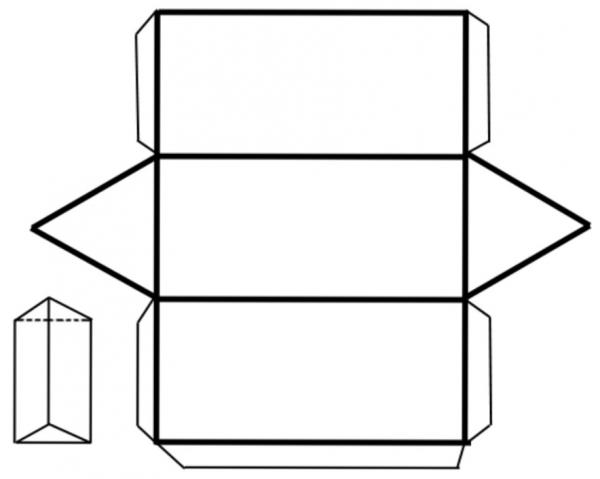
Видно, что вся поверхность образована двумя треугольниками и тремя прямоугольниками.

В случае призмы общего типа ее поверхность будет состоять из двух n-угольных оснований и n четырехугольников.

Рассмотрим подробнее вопрос вычисления площади поверхности призм разных типов.

Площадь основания призмы правильной

Пожалуй, самой простой задачей при работе с призмами является проблема нахождения площади основания правильной фигуры. Поскольку оно образовано n-угольником, у которого все углы и длины сторон являются одинаковыми, то всегда можно разделить его на одинаковые треугольники, у которых известны углы и стороны. Суммарная площадь треугольников будет площадью n-угольника.

Еще один способ определить часть площади поверхности призмы (основание) заключается в использовании известной формулы. Она имеет следующий вид:

S_n = n/4*a²*ctg(pi/n)

То есть площадь S_n n-угольника однозначно определяется исходя из знания длины его стороны a. Некоторую сложность при расчете по формуле может составить вычисление котангенса, особенно когда n>4 (для n≤4 значения котангенса - это табличные данные). Для определения этой тригонометрической функции рекомендуется воспользоваться калькулятором.

При постановке геометрической задачи следует быть внимательным, поскольку может потребоваться найти площадь оснований призмы. Тогда полученное по формуле значение следует умножить на два.

Площадь основания треугольной призмы

На примере треугольной призмы рассмотрим, как можно найти площадь основания этой фигуры.

Сначала рассмотрим простой случай - правильную призму. Площадь основания вычисляется по приведенной в пункте выше формуле, нужно подставить в нее n=3. Получаем:

S₃ = 3/4*a²*ctg(pi/3) = 3/4*a²*1/√3 = √3/4*a²

Остается подставить в выражение конкретные значения длины стороны a равностороннего треугольника, чтобы получить площадь одного основания.

Теперь предположим, что имеется призма, основание которой представляет собой произвольный треугольник. Известны две его стороны a и b и угол между ними α. Эта фигура изображена ниже.

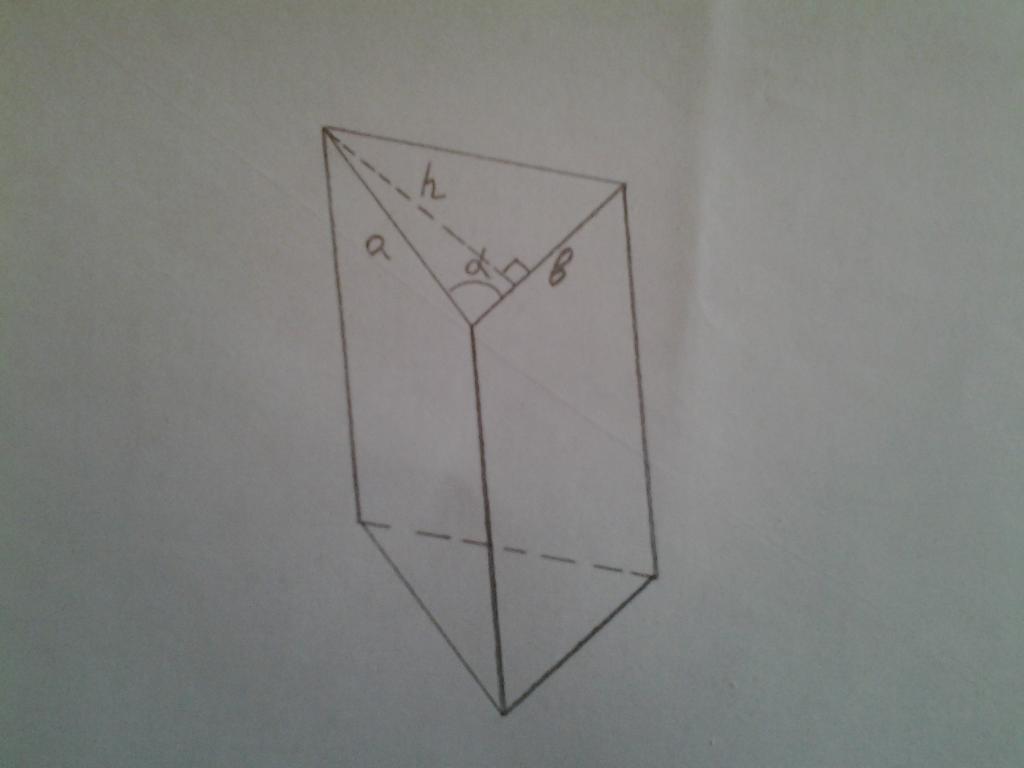
Как в этом случае найти площадь основания призмы треугольной? Необходимо вспомнить, что площадь любого треугольника равна половине произведения стороны и высоты, опущенной на эту сторону. На рисунке проведена высота h к стороне b. Длина h соответствует произведению синуса угла альфа на длину стороны a. Тогда площадь всего треугольника равна:

S = 1/2*b*h = 1/2*b*a*sin(α)

Это и есть площадь основания изображенной треугольной призмы.

Боковая поверхность

Мы разобрали, как найти площадь основания призмы. Боковая поверхность этой фигуры всегда состоит из параллелограммов. Для прямых призм параллелограммы становятся прямоугольниками, поэтому суммарную их площадь вычислить легко:

S = ∑_i=1ⁿ(a_i*b)

Здесь b - длина бокового ребра, a_i - длина стороны i-го прямоугольника, которая совпадает с длиной стороны n-угольника. В случае правильной n-угольной призмы получаем простое выражение:

S = n*a*b

Если призма является наклонной, тогда для определения площади ее боковой поверхности следует сделать перпендикулярный срез, рассчитать его периметр P_sr и умножить его на длину бокового ребра.

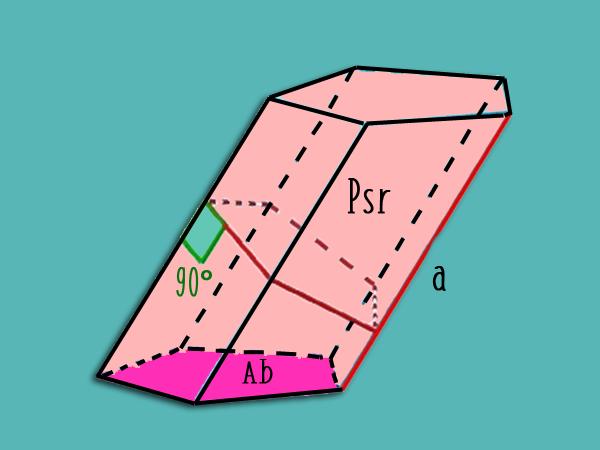
Рисунок выше показывает, как следует делать этот срез для наклонной пятиугольной призмы.