Как называется четырехугольник с прямыми углами?

Изучение геометрии начинается с рассмотрения простых фигур на плоскости, которые легко представить, используя абстрактное воображение. Одна из таких фигур - это четырехугольник с прямыми углами. В 3 классе общеобразовательных школ начинают знакомиться с ней и подробно исследуют ее свойства в старших классах. Рассмотрим главные характеристики этой фигуры в статье, а также приведем примеры ее использования в быту.

Как называется с прямыми углами четырехугольник?

Слово "четырехугольник" говорит о том, что рассматриваемая фигура состоит из четырех углов. На плоскости она будет замкнута только в том случае, если имеет четыре прямые стороны. Если противоположные стороны попарно друг другу параллельны, то такая фигура называется параллелограммом. Его четыре угла попарно равны, однако они могут принимать произвольные значения от 0^o до 180^o. Если все его углы будут равны 90^o, то они называются прямыми. Четырехугольник с углами прямыми - это прямоугольник, и одновременно он является параллелограммом.

Прямоугольник характеризуется всего двумя параметрами: длинами его соседних сторон. Далее в статье будем обозначать их a и b. Если эти длины равны друг другу, то прямоугольник вырождается в квадрат.

Формула для площади

Прямоугольник - это совершенная фигура, под которую человек в ходе своей жизнедеятельности старается подогнать окружающие объекты, например кирпич, форму двора перед домом, монитор компьютера и так далее. Поэтому часто возникает задача расчета площади прямоугольника.

Рассчитать площадь рассматриваемой фигуры не представляет никакой сложности. Поскольку прямоугольник - это параллелограмм, то его площадь вычисляется как произведение двух длин: высоты, опущенной на некоторую сторону, и этой стороны. Высота параллелограмма находится как произведение синуса одного из его углов на сторону. Поскольку мы рассматриваем конкретный вид параллелограмма - прямоугольник, то синус прямого угла равен единице, это означает, что искомая формула для площади принимает следующий вид:

S = a*b

Площадь четырехугольника с прямым углом равна произведению длин двух его непараллельных сторон.

Ниже будет показано, как найти площадь прямоугольника, если известны другие его элементы, например длина диагонали.

Диагонали прямоугольника

На рисунке ниже изображен произвольный четырехугольник с прямыми углами и его две диагонали.

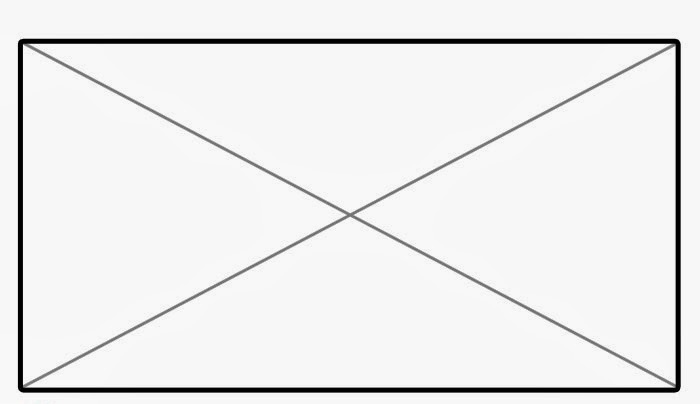
Видно, что диагонали разделяют на две части противоположные прямые углы фигуры. Будем обозначать точку пересечения диагоналей символом C. Она имеет важное значение, поскольку является центром симметрии фигуры. Длины обеих диагоналей равны.

Диагонали делят прямоугольник на четыре равнобедренных треугольника, для которых легко вычислить длины сторон и площадь. Каждые два треугольника, основания которых лежат на сторонах равной длины прямоугольника, являются одинаковыми.

Если провести одну диагональ, то она разделит прямоугольник на два совершенно одинаковых прямоугольных треугольника. Этот факт позволяет использовать тиорему Пифагора, чтобы рассчитать длину диагонали, зная катеты треугольника. Ниже рисунок показывает, как можно найти квадрат диагонали c прямоугольника. Здесь диагональ является гипотенузой, а стороны прямоугольника соответствуют катетам треугольника.

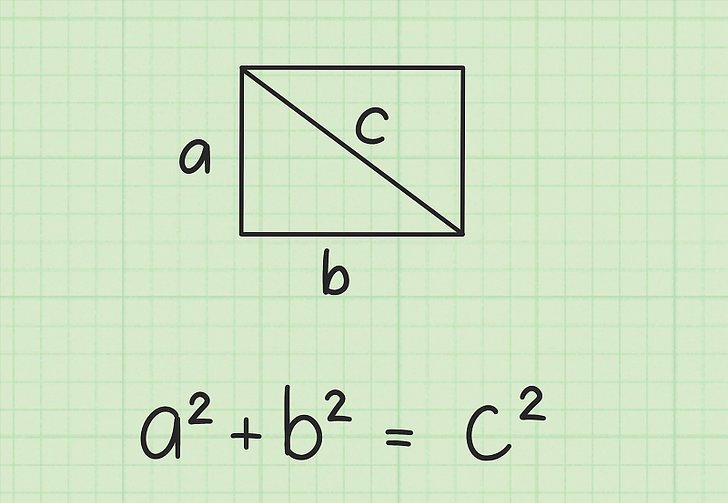
Тогда значение длины c будет равно:

c = √(a² + b²)

Симметрия прямоугольника

Как было отмечено, центр его симметрии - это точка C, образованная пересекающимися диагоналями. Рассматривая фигуру на плоскости, можно сказать, что ось, через эту точку проходящая и параллельная двум сторонам прямоугольника, является осью симметрии второго порядка, то есть поворот вокруг нее на 180^o переведет прямоугольник сам в себя. Поскольку рассматриваемый четырехугольник имеет две пары параллельных сторон, то очевидно, что он обладает двумя указанными осями симметрии.

Ось симметрии делит фигуру на два одинаковых прямоугольника со сторонами:

a и b/2 или b и a/2

Некоторые геометрические свойства прямоугольника

Поскольку рассматриваемая фигура обладает некоторой симметрией, имеет прямые углы и попарно параллельные стороны, то для нее можно выделить ряд важных свойств, используемых на практике. Перечислим их:

1. Всякая прямая, которая проходит через центр C фигуры, пересекает ее в двух точках, находящихся на одинаковом расстоянии от точки C. Максимальное расстояние от C до стороны диагонали прямоугольника равно половине длины его диагонали, минимальное же расстояние равно половине длины его меньшей стороны.
2. Если поделить одну сторону прямоугольника точкой пополам, то, соединяя эту точку с вершинами противоположной параллельной стороны, получаем равнобедренный треугольник с площадью, равной половине площади прямоугольника.
3. Если точку, описанную выше, смещать из центра стороны к одному или другому ее концу, то равнобедренность отмеченного треугольника будет нарушаться, однако его площадь будет оставаться неизменной.
4. Любой прямоугольник можно вписать в окружность.

Первое свойство является очевидным, поскольку любая прямая, проходящая через C, будет пересекать параллельные стороны фигуры. Докажем остальные свойства.

Доказательство свойств 2, 3 и 4

Рассмотрим сначала свойства 2 и 3. На рисунке ниже показан прямоугольник, на сторонах которого построены три треугольника:

ABC₁, ABC₂ и ABC₃

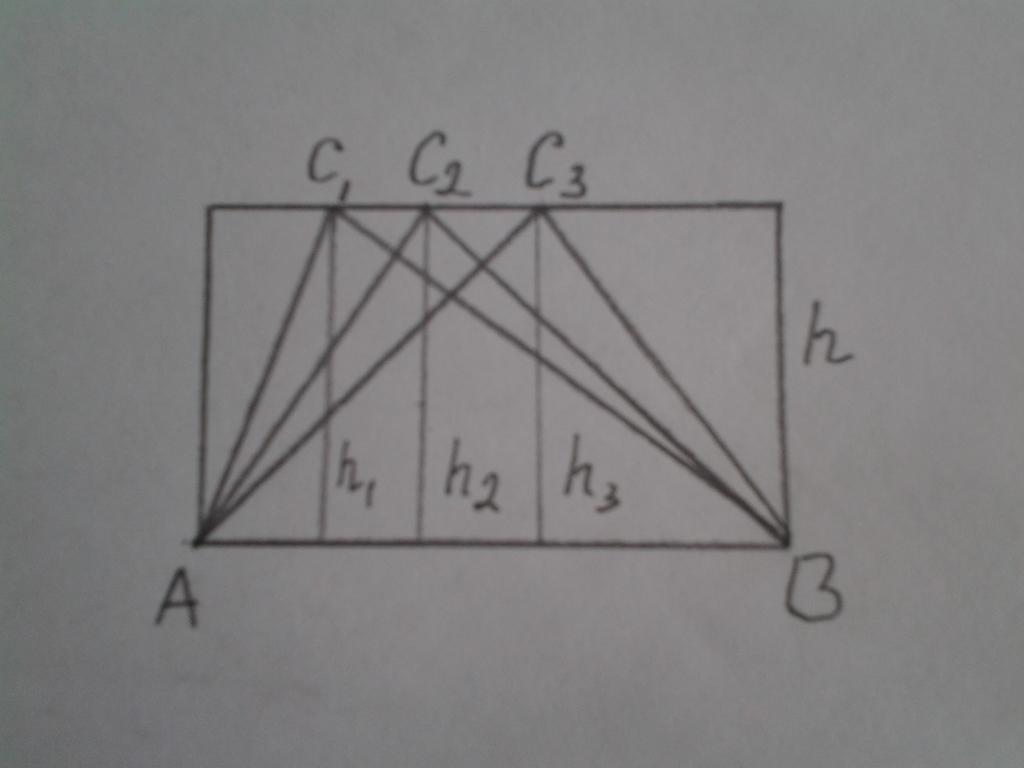
Согласно формуле нахождения площади треугольника, для них можно записать:

S₁ = 1/2*h₁*AB;

S₂ = 1/2*h₂*AB;

S₃ = 1/2*h₃*AB

Видно, что все высоты h_i рассматриваемых треугольников равны длине стороны h прямоугольника. Это означает, что и их площади равны:

S₁ = S₂ = S₃

Теперь запишем формулу для площади S прямоугольника и поделим S на площадь одного из изображенных треугольников, получим:

S = AB*h;

S/S₁ = AB*h/(1/2*h*AB) = 2

Таким образом, прямоугольник имеет площадь в два раза больше, чем любой из изображенных треугольников, то есть мы доказали второе и третье свойства.

Что касается возможности вписывания с прямыми углами четырехугольника в окружность, то здесь следует рассуждать так: проведем диагонали фигуры, они пересекутся в точке C. Поскольку эта точка находится на одинаковом расстоянии от четырех вершин прямоугольника, то она может служить центром окружности. Если радиус окружности равен половине длины диагонали, то линия окружности пройдет через все четыре вершины прямоугольника, то есть он окажется вписанным в нее.

Является ли четырехугольник, у которого один угол прямой, прямоугольником?

Ответ на вопрос будет положительным только в том случае, если рассматриваемый четырехугольник будет параллелограммом. В этом случае, если один угол равен 90^o, то два других смежных угла тоже будут прямыми, а значит, четвертый угол тоже будет равен 90^o. Мы нашли в четырехугольнике прямые углы все, значит он - прямоугольник.

В случае, если четырехугольник с одним прямым углом не будет иметь попарно параллельные стороны, то прямоугольником он не будет являться.

Где используется прямоугольник и его свойства?

При изготовлении тетрадных листов используют прямоугольную форму, причем отношение длин большей стороны к меньшей равно √2. Такая форма фигуры приводит к тому, что если ее поделить пополам симметричной осью, параллельной большей стороне, то у образованных двух новых прямоугольников отношение сторон также будет равно √2. Такое деление можно продолжать до бесконечности, при этом форма образующихся прямоугольников будет сохраняться.

Прямоугольная форма используется при производстве телевизионных экранов. До эры жидкокристаллических (ЖК) мониторов использовались электронно-лучевые экраны, отношение сторон которых было равно 4:3. С появлением ЖК-мониторов высокого разрешения, стали применять новый стандарт: 16:9.

Мозаика, которой украшают стены зданий, также имеет форму четырехугольника с прямыми углами.

Расчет площади фигуры по известной диагонали

Завершим статью рассмотрением вопроса вычисления площади четырехугольника, вершины прямых углов которого соединены диагональю. Рассчитаем площадь современного ЖК-монитора, если известно, что длина его диагонали с = 35 см.

Решить эту задачу можно потому, что монитор имеет стандартизированное отношение сторон, равное 16:9. Обозначая за x неизвестный коэффициент, получаем длины сторон монитора:

a = 16*x;

b = 9*x

Теперь применяем формулу для определения диагонали, получаем:

c² = a² + b² =>

35² = x²*(16²+9²) =>

x = 35/√(16²+9²) ≈ 1,9

Тогда стороны монитора и площадь его равны:

a = 16*x = 30,4 см;

b = 9*x = 17,1 см;

S = a*b ≈ 520 см²

Отметим еще раз, что определить по значению диагонали площадь можно только в том случае, если известно отношение сторон прямоугольника.