Понятие ускорения. Движение с постоянным ускорением. Формулы и пример задачи

Кинематика - это раздел механики движения в физике, который занимается исследованием и описанием перемещения тел. В данной статье приведены основные величины, что описывают механическое движение. Рассмотрим, что такое ускорение и движение с постоянным ускорением, приведем соответствующие формулы.

Три величины кинематики

Этими величинами являются путь L, скорость v¯ и ускорение a¯. Первая из них является скаляром и измеряется в метрах, вторая и третья - это величины векторные, которые выражаются в метрах в секунду и в метрах в квадратную секунду, соответственно. Все единицы соответствуют системе СИ.

Согласно определению, скорость - это быстрота перемещения тела в пространстве, то есть:

v¯ = dL/dt

В свою очередь, ускорение - это быстрота изменения скорости, что математически записывается так:

a¯ = dv¯/dt

Кинематические характеристики имеет смысл рассматривать применительно к данной траектории движения. Последняя может быть прямолинейной или криволинейной. От типа траектории зависит направление полного ускорения. Скорость же направлена к траектории всегда по касательной.

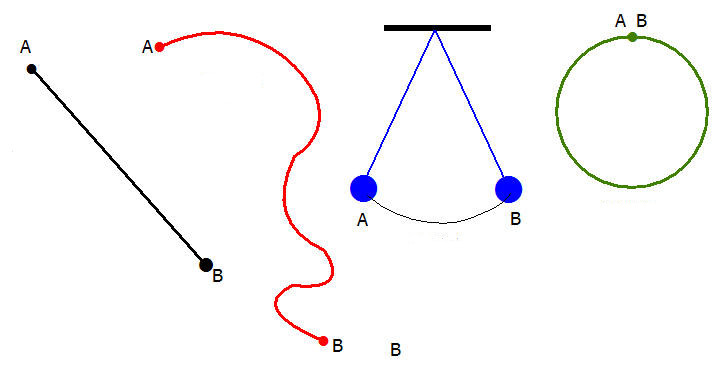
Особенности ускорения во время движения по кривой

Поскольку ускорение - это численная характеристика изменения скорости, то она однозначно описывает все аспекты этого изменения. Речь идет не только об абсолютной величине, но также и о векторе направления v¯. Изменение абсолютной величины скорости описывает тангенциальное, или касательное ускорение. Оно направлено или по вектору скорости, либо против него. Формула для его расчета имеет вид:

a_t = dv/dt

Поскольку тело перемещается по кривой, например по окружности, то величина v¯ постоянно меняет свое направление. Какова причина этого изменения? Она заключается в действии на тело нормального или центростремительного ускорения. Эта величина направлена перпендикулярно линии траектории и вычисляется по формуле:

a_n = v²/r

Где v - абсолютное значение скорости, r - кривизна траектории (радиус окружности).

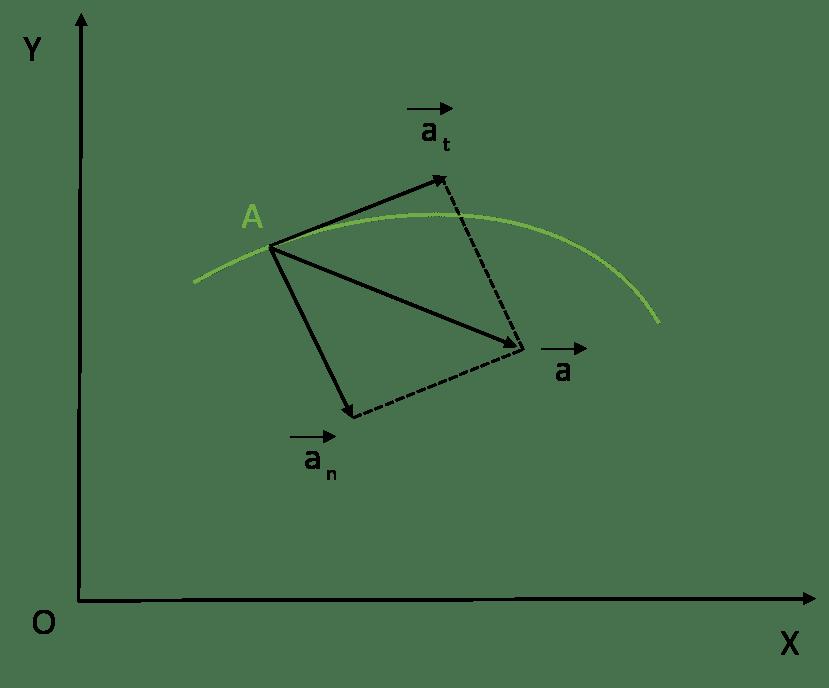
Обе составляющие полного ускорения a позволяют определить его с помощью такого равенства:

a = √(a_t² + a_n²)

Отметим, что движение по криволинейной траектории всегда предполагает наличие у тела двух компонентов ускорения.

Движение с постоянным ускорением по прямой

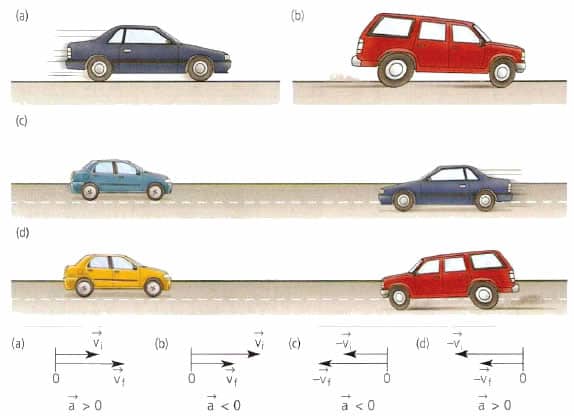
Если траектория является прямой линией, то изучение процесса движения значительно облегчается. Дело в том, что при таком движении скорость направлена всегда в одном направлении, а это означает, что нормальная компонента ускорения отсутствует. Полное ускорение при прямолинейном движении однозначно определяется его тангенциальной компонентой. Далее в статье будем рассматривать только движение по прямой, поэтому величину a будем называть просто ускорением.

Особое внимание заслуживает рассмотрение процесса перемещения тела по прямой, которое осуществляется с постоянным ускорением. Для такого перемещения просто записать математические уравнения движения. Они будут рассмотрены ниже.

Примерами движения тел с постоянным ускорением являются разгон автомобиля со старта, свободное падение тел в однородном поле гравитации, торможение транспортных средств.

Формулы для скорости

Рассматривая ускорение и движение с постоянным ускорением в 10 классе общеобразовательных школ, учащиеся знакомятся с формулами для определения скорости и пройденного пути. Начнем с формул для скорости.

Предположим, что тело находилось в состоянии покоя, затем оно начало движение с постоянным ускорением. Как при этом будет меняться его скорость? Ответ на этот вопрос содержит следующее равенство:

v = a*t

То есть скорость линейно будет возрастать. Коэффициентом пропорциональности между величинами v и t является ускорение a.

Теперь представим ситуацию, что тело двигалось с постоянной скоростью v₀, а затем начало ускоряться. Как изменится при этом предыдущая формула для скорости? Она примет вид:

v = v₀ + a*t.

Отметим, что отсчет времени в этой формуле начинается с момента появления у тела ускорения.

Теперь предположим третий вариант: вместо ускорения движения в предыдущем примере тело начало замедляться. В такой ситуации следует использовать выражение:

v = v₀ - a*t.

Во всех трех случаях графиками скорости от времени являются прямые линии.

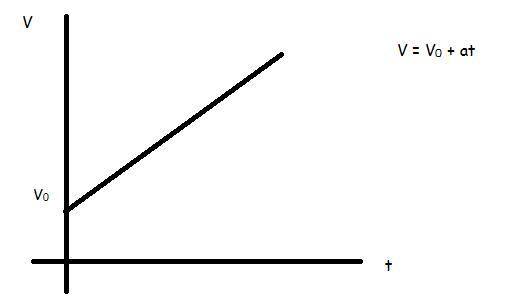
Формулы для пути

Рассматривая тему ускорения и движения с постоянным ускорением прямолинейное, необходимо также привести формулы для пройденного телом пути. В конечном счете на практике именно эта кинематическая величина имеет смысл.

Соответствующие формулы для L можно получить, если взять интеграл по времени для приведенных выше выражений для скоростей. Три формулы записаны ниже:

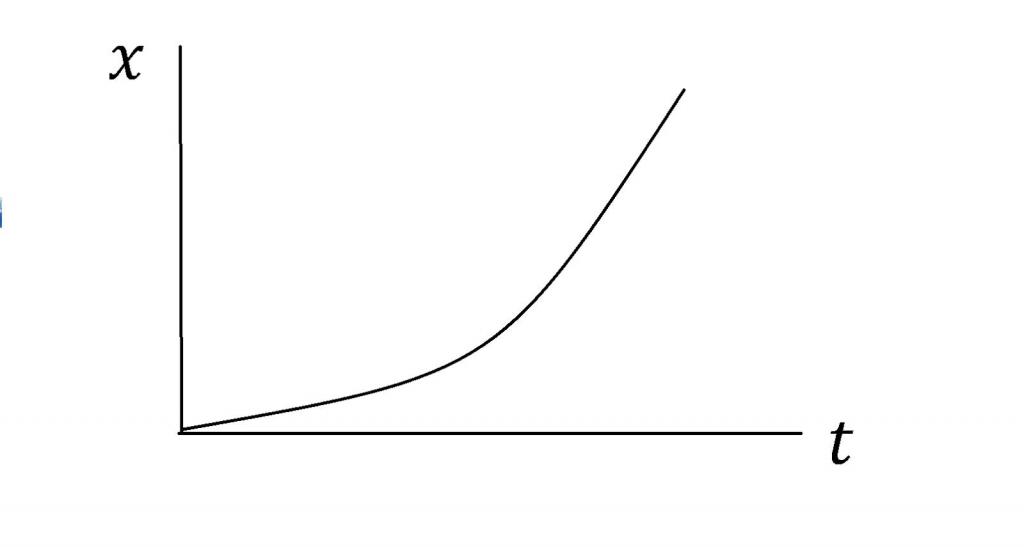
L = a*t²/2;

L = v₀*t + a*t²/2;

L = v₀*t - a*t²/2

Первое выражение определяет путь для чистого движения с неизменным ускорением, второе равенство описывает ускоренное движение с ненулевой начальной скоростью, третья формула используется для вычисления пути торможения при равнозамедленном движении.

Задача с подъемом тела в гравитационном поле

Как выше было отмечено, свободное падение происходит с постоянным ускорением. Движение с ускорением постоянным характеризуется величиной g, которая вблизи поверхности нашей планеты равна 9,81 м/с².

Известно, что тело было брошено вверх вертикально. Начальная скорость равна 30 м/с. Необходимо вычислить высоту, на которую тело поднимется.

Данная задача является типичной проблемой на равнозамедленное перемещение по прямой линии. Обозначим высоту подъема буквой h. Она будет равна пути, который тело пролетит до момента его полной остановки в высоте. Эта высота равна:

h = v₀*t - g*t²/2

Время полета можно определить из условия равенства величины v нулю в точке максимальной высоты, то есть:

v = v₀ - g*t = 0 =>

t = v₀/g

Подставляя равенство для t в формулу для h, получаем:

h = v₀²/g - g*(v₀/g)²/2 = v₀²/(2*g)

Подставляя значение начальной скорости, приходим к ответу: h = 45,9 метра.