Изохорная и изобарная теплоемкости воздуха. Пример задачи

Термодинамика газов является специальным разделом физики, который изучает и исследует поведение газовых систем при различных внешних условиях. В данной статье рассмотрим вопрос теплоемкости воздуха с использованием модели идеального газа.

Воздух - идеальный газ

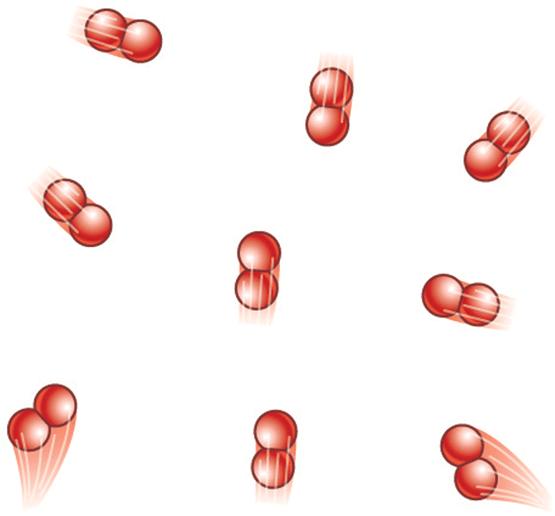
Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.

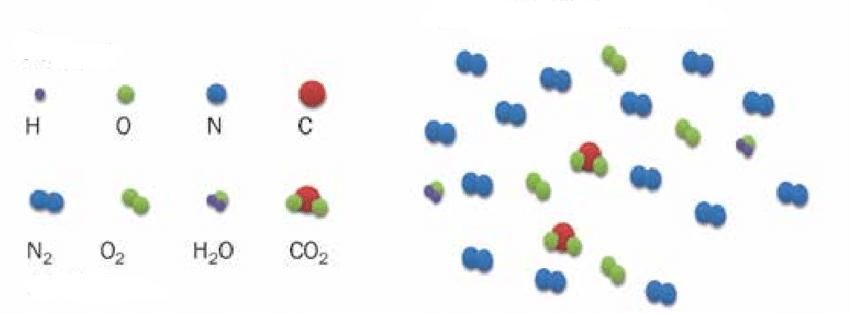
Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.

Теплоемкость и ее виды

Согласно физическому определению, теплоемкость - это величина, показывающая, сколько нужно на систему затратить теплоты, чтобы ее нагреть на 1 градус Цельсия или на 1 кельвин. Поскольку процессы нагревания и охлаждения являются обратимыми, то при охлаждении системы на 1 градус выделяется количество теплоты, равное ее теплоемкости.

Как физическая величина теплоемкость может быть абсолютной, молярной или массовой. Определение абсолютной теплоемкости для произвольной системы было дано выше. Молярной называется теплоемкость на 1 моль газа, массовой - на 1 кг газа. Молярная величина чаще используется для рассматриваемого агрегатного состояния материи.

В зависимости от изопроцесса, при котором измеряют теплоемкость, она бывает изохорной и изобарной. В первом случае в системе с газом не изменяется объем, во втором случае сохраняется давление.

Формулы изохорной и изобарной теплоемкостей воздуха

Сначала рассмотрим изохорную величину. Обозначим ее C_V. Первое начало термодинамики, которое следует из закона сохранения энергии, для изохорного процесса выглядит следующим образом:

H = dU

То есть все тепло H, подводимое к системе, идет на увеличение ее внутренней энергии. Изменение величины U можно записать так:

dU = C_V*dT

С другой стороны, если воспользоваться универсальным уравнением состояния идеальной газовой системы, то формула для dU запишется в виде:

dU = z/2*n*R*dT

Здесь z - количество степеней свободы молекул, n - количество вещества, R - постоянная, dT - изменение температуры. Выражение выше следует из того факта, что внутренняя энергия идеального газа в точности равна кинетической энергии его молекул.

Из сравнения двух равенств получаем формулу для изохорной теплоемкости:

C_V = z/2*n*R

В случае воздуха z=5, поскольку он на 99 % состоит из двухатомных молекул азота и кислорода (двухатомные молекулы имеют 3 поступательные и 2 вращательные степени свободы). Полагая n=1 моль, приходим к формуле изохорной молярной теплоемкости воздуха:

C_V = 5/2*R = 2,5*R

Напомним, что постоянная R равна 8,314, тогда C_V = 20,785 Дж/(моль*К).

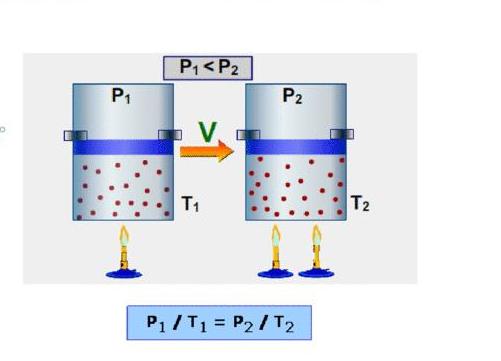
Теперь определим молярную изобарную теплоемкость воздуха. Поскольку в результате изобарного нагрева газ расширяется, то он выполняет некоторую работу. Первое начало термодинамики в этом случае принимает вид:

H = dU + P*dV

Энтальпия H через изобарную теплоемкость C_P для 1 моль вещества запишется так:

H = C_P*dT

Работу газа с использованием уравнения Клапейрона-Менделеева можно записать так:

P*dV = R*dT

Эти выражения позволяют записать следующее соотношение изобарной и изохорной теплоемкостей:

C_P = C_V + R

Подставляя величину C_V для воздуха, получаем изобарную молярную теплоемкость для него:

C_P = 2,5*R + R = 3,5*R = 29,099 Дж/(моль*К)

Таким образом, величина C_P оказывается больше, чем C_V.

Пример решения задачи

В цилиндре под поршнем находятся 3 моль воздуха при атмосферном давлении. В процессе нагрева цилиндра поршень стал подниматься, сохраняя постоянное давление в системе. Чему равна работа газа при расширении, если известно, что его конечная температура стала больше начальной на 10 ^oC?

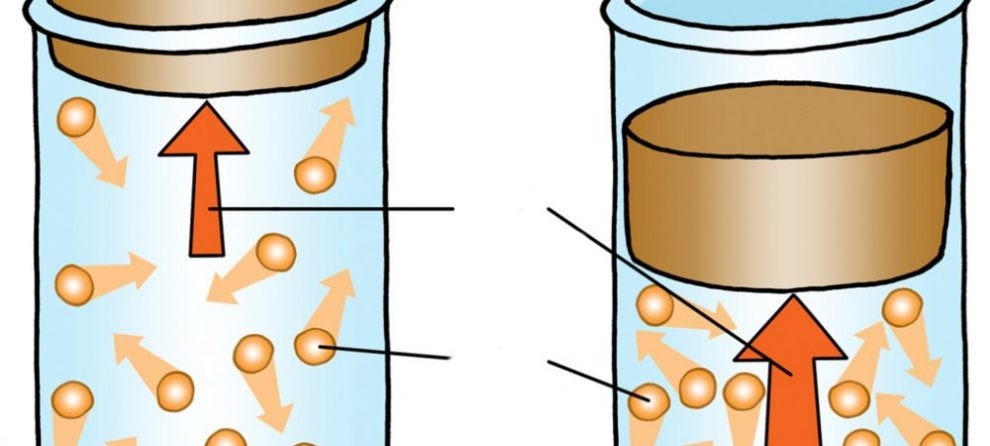
Воспользуемся первым законом термодинамики для изобарного нагрева:

n*C_P*dT = n*C_V*dT + P*dV

Отсюда работа газа (третье слагаемое) выразится так:

P*dV = n*(C_P - C_V)*dT

Подставляя данные из условия задачи, а также значения молярных теплоемкостей воздуха, получаем ответ: воздух в цилиндре, расширяясь, совершит работу 249,42 Дж.