Таблица тангенсов углов: полный справочник значений

Тригонометрические функции, в частности тангенс угла, широко применяются в математике, физике, инженерных расчетах. Знание точных значений тангенсов позволяет быстро и качественно решать многие практические задачи. В этой статье мы подробно разберем, что такое тангенс, рассмотрим полную таблицу его значений и приведем примеры использования.

Определение

Тангенс угла равен отношению синуса этого угла к его косинусу. Геометрически в прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему.

Тангенс определен для всех углов, кроме кратных 90° (π/2 + kπ, где k - целое число). В этих точках происходит разрыв функции.

Таблица значений тангенсов углов

Рассмотрим подробную таблицу значений тангенсов для углов.

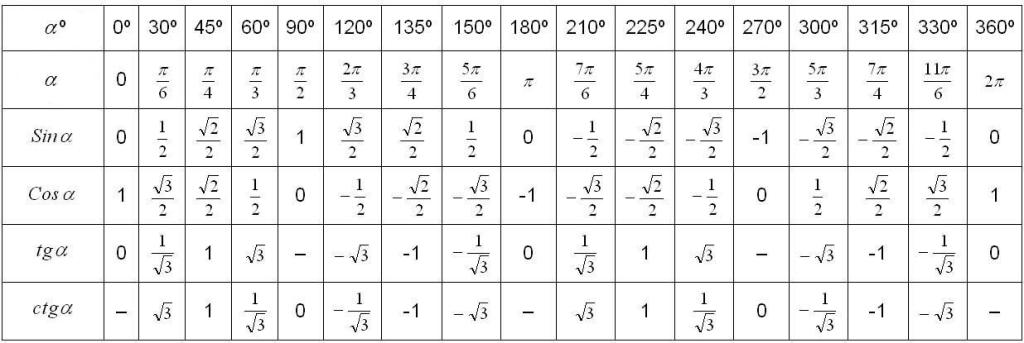
Для упрощения вычислений полезно запомнить значения тангенса для некоторых часто встречающихся углов: 0°, 30°, 45°, 60°, 90°.

Вычисление тангенсов на практике

При решении задач на вычисление тангенсов углов можно использовать разные подходы.

С помощью инженерного калькулятора значение тангенса любого угла может быть найдено за считанные секунды. Достаточно ввести величину угла и нажать кнопку "tan".

Если под рукой нет калькулятора, выручит таблица тангенсов. Как мы видели выше, табличные значения имеют шаг 1° и позволяют точно найти тангенс для любого угла от 0° до 90°.

Для часто встречающихся значений углов 30°, 45°, 60° лучше запомнить тангенсы:

tg 30° = 0.577
tg 45° = 1 tg 60° = 1.732

Это позволит быстро решать типовые задачи.

Таким образом, зная таблицу тангенсов и владея основными способами вычисления, можно с легкостью находить tg любых необходимых углов.

Рассмотрим несколько практических примеров, где используются значения тангенсов углов.

Вычисление длин сторон треугольника

Допустим, дан прямоугольный треугольник с углом 30° и гипотенузой, равной 10 см. Требуется найти длины катетов.

Известно, что tg 30° = 0.577. Следовательно:

• sin 30° = 0.5
• cos 30° = 0.866

По теореме Пифагора:

• Катет а = 10 * sin 30° = 5 см
• Катет b = 10 * cos 30° = 8.66 см

Ответ: а = 5 см, b = 8.66 см.

Расчет угла наклона плоскости

Пусть требуется определить угол наклона плоскости, если отношение высоты к длине основания равно tg 60° = 1.732.

Из таблицы тангенсов находим, что угол наклона плоскости равен 60°.

Зная tg угла наклона винтовой линии, можно рассчитать шаг резьбы винта, используя соотношения между основными геометрическими параметрами резьбы.

Удобным инструментом для вычисления тангенсов углов являются онлайн-калькуляторы. Достаточно ввести значение угла в градусах или радианах, и калькулятор мгновенно вычислит тангенс.

Запоминание основных значений

Для быстрых вычислений в уме полезно запомнить значения tg наиболее часто используемых углов:

• tg 0° = 0
• tg 30° = 0.577
• tg 45° = 1
• tg 60° = 1.732

Эти значения пригодятся при решении многих типовых задач с использованием тангенсов.