Введение в динамическое программирование

Среди задач, решаемых с помощью математического программирования, можно выделить отдельный класс задач, требующих оптимизации многошаговых (многоэтапных) процессов. Такие задачи отличаются возможностью разбиения решения на несколько взаимосвязанных этапов. Для решения подобных задач используется динамическое программирование или, как его еще называют, многоэтапное программирование. Его методы оптимизированы для поиска оптимального решения многошаговых задач, которые можно разделить на несколько этапов, шагов и т. д.

Происхождение термина

Использование в названии слова «динамический» первоначально предполагало, что разделение на подзадачи будет происходить в основном во времени. При использовании динамических методов для решения производственных, хозяйственных и иных задач, в которых фигурирует временной фактор, разбивание на отдельные этапы не составляет труда. Но использовать технику динамического программирования возможно и в задачах, где отдельные этапы не связаны по времени. Всегда в многошаговой задаче можно выделить параметр или свойство, по которому можно произвести разделение на отдельные шаги.

Алгоритм (метод) решения многоэтапных задач

Алгоритм или метод динамического программирования основан на использовании принципа последовательного оптимизирования задачи, когда решение общей задачи разбивается на ряд решений отдельных подзадач с последующим объединением в единое решение. Очень часто отдельные подзадачи оказываются одинаковыми, и одно общее решение значительно сокращает время расчета.

Особенностью метода является автономность решения задачи на каждом отдельном этапе, т. е. независимо от того, как оптимизировался и решался процесс на предыдущем этапе, в текущем расчете используются только параметры процесса, характеризующие его в данный момент. Например, водитель, двигающийся по дороге, принимает решение о текущем повороте независимо от того, как и сколько он ехал до этого.

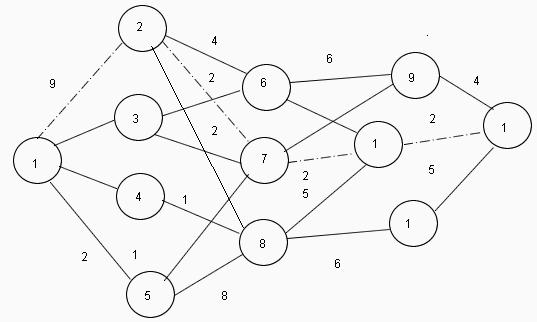
Метод сверху и метод снизу

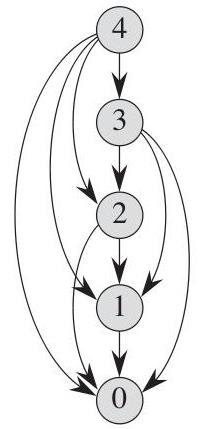
Несмотря то что при расчете на отдельном этапе решения задачи используются параметры процесса на текущий момент, результат оптимизации на предыдущем этапе влияет на расчеты последующих этапов для достижения наилучшего результата в целом. Динамическое программирование называет такой принцип решения методом оптимальности, который определяет, что оптимальная стратегия решения задачи вне зависимости от начальных решений и условий должна последующими решениями на всех этапах составить оптимальную стратегию относительно первоначального состояния. Как видим, процесс решения задачи представляет собой непрерывную оптимизацию результата на каждом отдельном этапе от первого до последнего. Такой метод называется методом программирования сверху. На рисунке схематически показан алгоритм решения сверху вниз. Но существует класс многошаговых задач, в которых максимальный эффект на последнем этапе уже известен, например, мы уже приехали из пункта А в пункт Б и теперь хотим узнать, правильно мы ехали на каждом предыдущем этапе или можно было что-то сделать более оптимально. Возникает рекурсивная последовательность этапов, т. е. мы идем как бы «от обратного». Этот метод решения получил название "метод программирования снизу".

Практическое применение

Динамическое программирование может использоваться в любой сфере деятельности, где присутствуют процессы, которые можно по какому-либо параметру (время, сумма, температура и т. д.) разделить на ряд одинаковых небольших этапов. Наибольшее применение динамические способы решения получили в теории управления и при разработке вычислительных систем.

Поиск оптимального пути

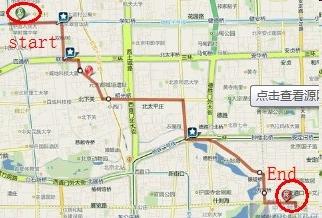
С помощью динамической оптимизации возможно решение широкого класса задач по нахождению или оптимизации кратчайшего пути и других задач, в которых «классический» метод перебора возможных вариантов решения приводит к увеличению времени расчета, а иногда вообще неприемлем. Классическая задача динамического программирования - это задача о рюкзаке: дано некоторое количество предметов с определенной массой и стоимостью, и необходимо выбрать набор предметов с максимальной стоимостью и массой, не превосходящий объем рюкзака. Классический перебор всех вариантов в поисках оптимального решения займет значительное время, а с помощью динамических методов задача решается в приемлемые сроки. Задачи поиска кратчайшего пути для транспортной логистики являются основными, и динамические методы решения оптимально подходят для их решения. Наиболее простым примером такой задачи является построение кратчайшего маршрута автомобильным GPS-навигатором.

Производство

Динамическое программирование широко используется при решении разнообразных производственных задач, таких как управление складскими запасами для поддержания нужного количества комплектующих в любой момент времени, календарное планирование производственного процесса, текущий и капитальный ремонт оборудования, равномерная загрузка персонала, максимально эффективное распределение инвестиционных средств и т. д. Для решения производственных задач методами динамического программирования разработаны специальные программные пакеты, интегрированные в популярные системы управления предприятиями, такие как SAP.

Научная сфера

Методы динамического программирования широко применяются в различных научных исследованиях. Например, они успешно используются в алгоритмах распознавания речи и образов, при обработке больших массивов данных в социологии и хозяйственной деятельности.