Гипотеза Пуанкаре: история проблемы, доказательство, смысл

По школьному курсу каждый знаком с понятиями теоремы и гипотезы. Как правило, в жизни затрагиваются самые простые и примитивные законы, в то время как математики делают очень сложные предположения и ставят интересные проблемы. Далеко не всегда им самим удается найти решения и доказательства, а в некоторых случаях над этим многие годы бьются их последователи и просто коллеги.

Институт Клея в 2000 году сформировал список из 7 так называемых Проблем Тысячелетия по аналогии с перечнем гипотез, составленным в 1900 году. Те задачи почти все оказались к настоящему времени решены, только одна из них перекочевала в обновленную версию. Сейчас список проблем выглядит следующим образом:

• гипотеза Ходжа;
• равенство классов P и NP;
• гипотеза Пуанкаре;
• теория Янга-Миллса;
• гипотеза Римана;
• существование и гладкость решения уравнений Навье-Стокса;
• гипотеза Берча-Свиннертон-Дайера.

Все они относятся к различным дисциплинам внутри математики и имеют важное значение. Например, уравнения Навье-Стокса относятся к гидродинамике, а на практике могут описать поведение вещества в земной магме или пригодиться в предсказании погоды. Но все эти проблемы все еще ищут своего доказательства или опровержения. Кроме одной.

Теорема Пуанкаре

Объяснить простыми словами, в чем заключается эта проблема, довольно непросто, но попробовать можно. Представим себе сферу, к примеру, мыльный пузырь. Все точки его поверхности равноудалены от его центра, который ей не принадлежит. Но это двумерное тело, а гипотеза говорит о трехмерном. Это представить уже невозможно, но на то у нас и есть теоретическая математика. При этом, разумеется, все точки этого тела также будут удалены от центра.

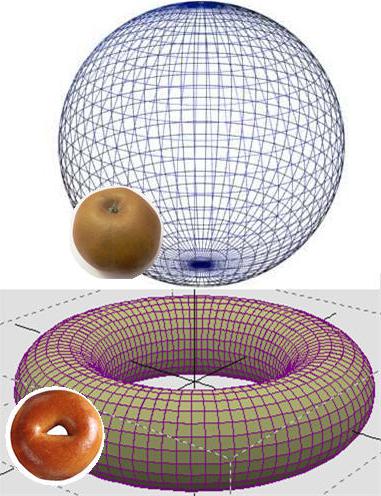
Эта проблема относится к топологии - науке о свойствах геометрических фигур. И одним из базовых терминов в ней является гомеоморфность, то есть высокая степень схожести. Чтобы привести пример, можно представить шар и тор. Одну фигуру никак нельзя получить из другой, избежав разрывов, а вот конус, куб или цилиндр из первого получатся довольно легко. Вот гипотеза Пуанкаре и посвящена этим метаморфозам с одной лишь разницей - речь идет о многомерном пространстве и телах.

История

Французский математик Анри Пуанкаре занимался самыми разными областями науки. О его достижениях может сказать, к примеру, тот факт, что совершенно независимо от Альберта Эйнштейна он выдвинул основные положения специальной теории относительности. В 1904 году он поднял проблему доказательства того, что любое трехмерное тело, обладающее некоторыми свойствами сферы, ею и является с точностью до деформации. Позднее она была расширена и обобщена, и стала частным случаем гипотезы Терстона, сформулированной в 1982 году.

Формулировка

Пуанкаре изначально оставил такое утверждение: всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. В дальнейшем оно было расширено и обобщено. И все же на протяжении длительного времени именно изначальная задача вызывала больше всего проблем, и была решена лишь через 100 лет после ее появления.

Интерпретация и смысл

О том, что такое гомеоморфность, речь уже шла. Теперь стоит поговорить о компактности и односвязности. Первое означает лишь, что многообразие имеет ограниченные размеры, не может быть непрерывно и бесконечно растянуто.

Что касается односвязаности, можно попробовать привести простой пример. Двумерная сфера - яблоко - обладает одним интересным свойством. Если взять обычную замкнутую резинку и приложить ее к поверхности, то плавной деформацией ее можно свести в одну точку. Это и есть свойство односвязаности, но представить его применительно к трехмерному пространству довольно затруднительно.

Если говорить совсем просто, проблематика заключалась в том, чтобы доказать, что односвязность - уникальное для сферы свойство. И если, условно говоря, опыт с резинкой завершился с таким результатом, то тело гомеоморфно ей. Что же касается приложения этой теории к жизни, Пуанкаре считал, что Вселенная в некотором смысле и является трехмерной сферой.

Доказательство

Не стоит думать, что из десятков математиков, работавших по всему миру, никто не продвинулся ни на йоту, занимаясь этой проблемой. Наоборот, прогресс был, и в конце концов он привел к результату. Сам Пуанкаре не успел закончить работу, но его исследования серьезно продвинули всю топологию.

В 1930-х годах интерес к гипотезе вернулся. Прежде всего, формулировка была расширена до "n-мерного пространства", а потом американец Уайтхед сообщил об успешном доказательстве, позднее отказавшись от него. В 60-70-х сразу два математика - Смейл и Столлингс - практически одновременно, но разными способами разработали решение для всех n больше 4.

В 1982 году и для 4 было найдено доказательство, оставалось только 3. В том же году Терстон сформулирован гипотезу о геометризации, при этом теория Пуанкаре стала ее частным случаем.

Дальше работа несколько застопорилась - американец Ричард Гамильтон предложил использовать в решении поток Риччи, но столкнулся с трудностями и не завершил исследования.

На 20 лет гипотеза Пуанкаре была как будто забыта. В 2002 году российский математик Григорий Перельман представил решение в общих чертах, спустя полгода сделав некоторые дополнения. Уже позже это доказательство проверяли и доводили "до блеска" американские и китайские ученые. А сам Перельман словно потерял к проблеме весь интерес, хотя он решил более общую задачу о геометризации, для которой гипотеза Пуанкаре является лишь частным случаем.

Признание и оценки

Разумеется, это сразу стало сенсацией, ведь решение одной из Проблем Тысячелетия просто не могло оказаться незамеченным. Еще больше удивления вызывал тот факт, что Григорий Перельман отказался от всех наград и премий, сообщив, что ему и так прекрасно живется. В умах обывателей он сразу стал примером того самого полусумасшедшего гения, которого интересует только наука.

Все это вызвало много обсуждений в прессе и СМИ, что популярность математика стала его тяготить. Летом 2014 года прошла информация о том, что Перельман уехал работать в Швецию, но это оказалось лишь слухами, он все еще скромно живет в Санкт-Петербурге и почти ни с кем не общается. Среди наград, присужденных ему, были не только премия института Клея, но и престижная медаль Филдса, но он отказался от всего. Впрочем, Гамильтон, который по оценкам Перельмана сделал не меньший вклад в доказательство, тоже не был забыт. В 2009 и 2011 годах он также удостоился некоторых престижных наград и премий.

Отражение в культуре

Несмотря на то что для простых обывателей как постановка, так и решение этой проблемы представляют мало смысла, о доказательстве стало известно довольно быстро. В 2008 году по этому поводу японским режиссером Масахито Касуга был снят документальный фильм "Чары гипотезы Пуанкаре", посвященный столетним попыткам решить эту задачу.

В съемках приняли участие многие математики, занимавшиеся этой проблемой, но вот главный герой - Григорий Перельман - сделать этого не захотел. Более или менее близкие его знакомые также были задействованы в съемках. Документальный фильм, выйдя на экраны на волне общественного резонанса по поводу отказа ученого принять премию, в определенных кругах снискал славу, а также получил несколько наград. Что же касается массовой культуры, простые люди до сих пор гадают, какими доводами руководствовался петербургский математик, отказавшись взять деньги, когда он мог отдать их, например, на благотворительность.