Зубчатое колесо. Основные параметры. Чертеж

Ни один хороший механизм не может быть построен без такой детали, как зубчатое колесо (или, иначе, шестерня). Правильное понимание того, как шестерни влияют на такие параметры, как крутящий момент и скорость вращения, очень важно. Ниже будет рассказано об азах зубчатых передач и о том, как правильно их использовать.

Механическое преимущество: крутящий момент против скорости вращения

Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.

Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.

Уравнение зубчатой передачи

Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:

Момент _{входной} * Скорость _{входная} = Момент _{выходной} * Скорость _{выходная}

Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.

Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:

0,5 Н∙м * 50 об/с = Момент _{выходной}* 5 об/с.

Ваш выходной крутящий момент будет 5 Н∙м.

Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению

0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость _{выходная},

Скорость _{выходная} = 5 об/с.

Итак, вы определили, используя простое уравнение, что при показателе Момент _{выходной} =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.

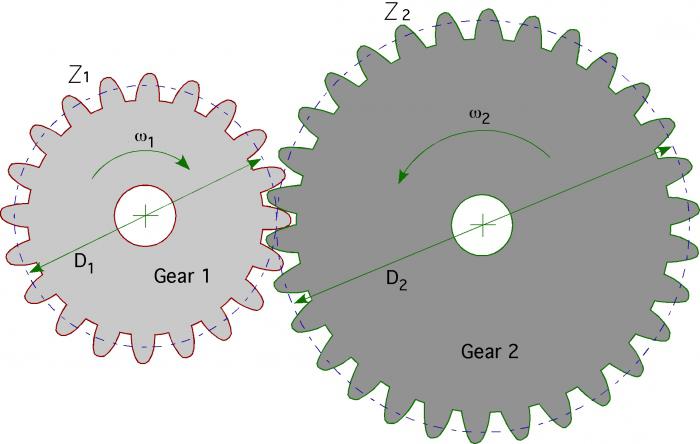
Передаточное число зубчатой передачи

Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.

Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.

Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.

Пример:

Момент _{входной} = 1,5 Н∙м, Скорость _{входная} = 100 об/с,

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная} * 3/2 = 150 об/с.

Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.

Достижение определенного передаточного числа

Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).

Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая - 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.

Эффективность передач

К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.

Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно ~ 90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.

Если (из предыдущего примера):

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная} * 3/2 = 150 об/с,

то тогда:

Истинный Момент _{выходной} = 1 Н∙м * 0,9= 0,9 Н∙м,

Истинная Скорость _{выходная} = 150 об/с * 0,9 = 135 об/с.

Направление вращения шестерен

Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.

Конструкция и параметры зубчатого колеса

Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.

Делительная окружность показана на нем пунктиром. По ней принято определять окружной шаг зубьев p (шаг зацепления), т. е. часть ее длины, приходящуюся на один зуб, и модуль шестерни m – часть диаметра делительной окружности d, приходящуюся на один зуб. Чтобы его вычислить, просто используйте формулу ниже:

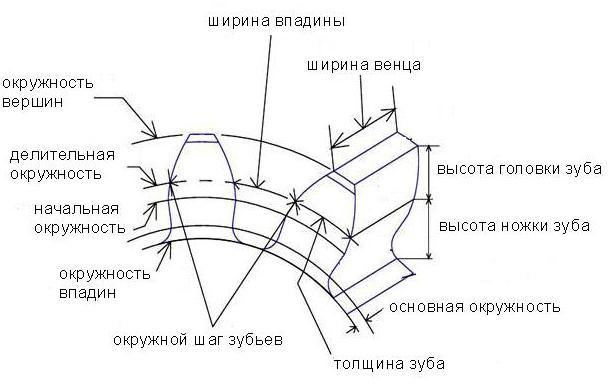
m = d/z= p/3,14, мм.

Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.

Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.

Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.

Расчет зубчатого колеса

Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.

1. Определение передаточного числа u.

2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.

3. Расчет зубьев передачи на изгиб.

4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).

5. Определение межосевого расстояния a_W из условия контактной прочности и округление его значения до стандартного.

6. Задание модуля из соотношения m = (0,01 - 0,02) х a_W и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.

7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.

8. Выбор коэффициентов формы зубьев для шестерни и колеса.

9. Проверка прочности зубьев по напряжениям изгиба.

10. Проведение геометрического расчета передачи.

11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.

Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.

Как обозначается точность изготовления зубчатых колес

При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:

• кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
• погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
• погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
• боковой зазор между неработающими поверхностями зубьев.

Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:

• вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
• допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.

Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.

Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:

8-Ас ГОСТ 1643 – 81.

Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:

5-4-3-Са ГОСТ 1643 – 81.

Типы зубчатых передач

Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.

Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.

Цилиндрические прямозубые колеса (КПД ~ 90%)

Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.

Цилиндрические косозубые колеса (КПД ~ 80%)

Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.

Цилиндрические шевронные колеса

Являются разновидностью предыдущего вида. Чем отличается такое зубчатое колесо. Чертеж его показан ниже. Видно, что по ширине его венца расположены зубья с правым и левым наклоном, так что такие составные зубья зубчатого колеса по форме напоминает «шевроны». Эти колеса обладают всеми преимуществами косозубого их вида, плюс отсутствием осевых нагрузок. Они способны самоцентрироваться и не нуждаются в дорогостоящих радиально-упорных подшипниках для восприятия осевых нагрузок.

Конические зубчатые колеса (КПД ~ 70%)

Зубья этих колес, располагающиеся на конических поверхностях, выполняют прямыми, косыми, круговыми (дугообразными). Эти передачи применяют для передачи момента между перекрещивающимися под разными углами валами. К сожалению, их КПД довольно низок, поэтому следует избегать их применения, если возможно.

Червячные передачи (КПД ~ 70%)

Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).

Еще одним преимуществом червячной передачи является то, что у нее только одно направление вращения. Это означает, что только приводной двигатель может вращать такую передачу, в то время как сила тяжести или другие сторонние силы не вызовут каких-либо вращений. Это бывает полезно, например, для стопорения груза на высоте.