Равномерное движение. Формула равномерного движения.

Знакомство с классическим курсом физики начинается с простейших законов, которым подчиняются тела, перемещающиеся в пространстве. Прямолинейное равномерное движение – самый простой вид изменения положения тела в пространстве. Такое движение изучается в разделе кинематики.

Противник Аристотеля

Галилео Галилей остался в анналах истории как один из величайших естествоиспытателей времен позднего Ренессанса. Он отважился проверять утверждения Аристотеля – неслыханная по тем временам ересь, ибо учение этого древнего мудреца всячески поддерживалось церковью. Идея равномерного движения тогда не рассматривалась – тело или двигалось «вообще», или находилось в состоянии покоя. Понадобились многочисленные эксперименты для того, чтобы объяснить природу движения.

Опыты Галилея

Классическим примером изучения движения стал известный эксперимент Галилея, когда он бросал различные тяжести со знаменитой Пизанской башни. В результате этого эксперимента выяснилось, что тела, имеющие разные массы, падают с одинаковой скоростью. Позднее эксперимент был продолжен в горизонтальной плоскости. Галилей предложил, что любой шар при отсутствии трения будет катиться с горки сколь угодно долго, при этом скорость его так же будет постоянной. Так, экспериментальным путем, Галилео Галилей открыл сущность первого закона Ньютона – при отсутствии внешних сил тело движется по прямой с постоянной скоростью. Прямолинейное равномерное движение – это и есть выражение первого закона Ньютона. В настоящее время различными видами движения занимается особый раздел физики - кинематика. В переводе с греческого данное наименование означает - учение о движении.

Новая система координат

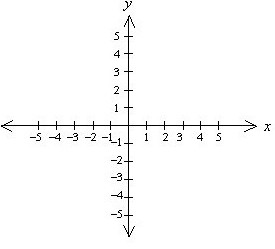
Анализ равномерного движения был бы невозможен без создания нового принципа определения положения тел в пространстве. Сейчас мы называем его прямолинейной системой координат. Автор ее - известный философ и математик Рене Декарт, благодаря которому мы и называем систему координат декартовой. В таком виде очень удобно представлять траекторию движения тела в трехмерном пространстве и анализировать такое перемещения, привязывая положение тела к координатным осям. Прямоугольная система координат представляет собой две пересекающиеся под прямым углом прямые. Точка пересечения обычно принимается за начало отсчета измерений. Горизонтальная линия называется абсциссой, вертикальная – ординатой. Поскольку мы живем в трехмерном пространстве, к плоскостной системе координат добавляют и третью ось – ее называют аппликатой.

Определение скорости

Скорость невозможно измерить так, как мы измеряем расстояние и время. Это всегда величина производная, которая и записывается в виде соотношения. В самом общем виде скорость тела равна отношению пройденного расстояния к затраченному времени. Формула для скорости имеет вид:

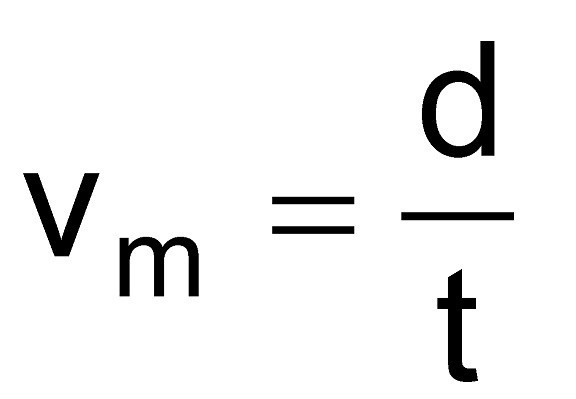
Где d- пройденное расстояние, t - затраченное время.

Направление напрямую влияет на векторное обозначение скорости (величина, определяющая время – скаляр, то есть оно направления не имеет).

Представление о равномерном движении

При равномерном движении тело движется вдоль прямой с постоянной скоростью. Поскольку скорость – это векторная величина, ее свойства описываются не только числом, но и направлением. Поэтому лучше уточнить определение, и сказать, что скорость равномерного прямолинейного движения постоянна по модулю и направлению. Чтобы описать прямолинейное равномерное движение, достаточно использовать декартову систему координат. В этом случае ось ОХ будет удобно проложить по направлению движения.

При равномерном перемещении положение тела в любой период времени определяется всего одной координатой - x. Направление движения тела и вектор скорости направлены вдоль оси х, при этом начало движения можно отсчитывать от нулевой отметки. Поэтому анализ перемещения тела в пространстве можно свести к проекции траектории движения на ось ОХ и описывать процесс алгебраическими уравнениями.

Равномерное движение с точки зрения алгебры

Допустим, что в определенный момент времени t₁ тело находится в точке на оси абсцисс, координата которой равна х₁. Черед некоторой промежуток времени тело изменит свое местоположение. Теперь координата его нахождения в пространстве будет равняться х₂. Сведя рассмотрение движения тела к его расположению на оси координат, можно определить, что путь, который прошло тело, равен разнице начальной и конечной координаты. Алгебраически это записывается так: Δs = x₂ – x_1.

Величина перемещения

Величина, определяющая перемещение тела, может быть и больше, и меньше 0. Все зависит от того, в какую сторону относительно направления оси перемещалось тело. В физике можно записывать и отрицательное, и положительное перемещение – все зависит от выбранной для отсчета системы координат. Прямолинейное равномерное движение происходит со скоростью, которая описывается формулой:

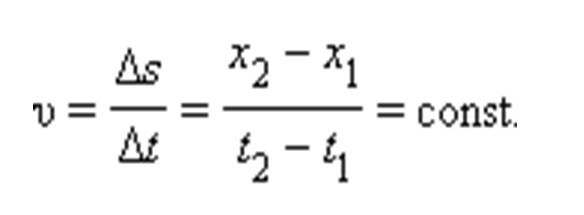
При этом скорость будет больше нуля, если тело движется вдоль оси ОХ от нуля; меньше нуля – если движение идет справа налево по оси абсцисс.

Такая краткая запись отражает суть равномерного прямолинейного движения – какими бы ни были изменения координат, скорость перемещения остается неизменной.

Галилею мы обязаны еще одной гениальной мыслью. Анализируя движение тела в мире, лишенном трения, ученый настаивал на том, что силы и скорости не зависят друг от друга. Эта блестящая догадка нашла свое отражение во всех существующих законах движения. Так, силы, действующие на тело, не зависят друг от друга и действуют так, будто других не существует. Применяя это правило к анализу движения тела, Галилей понял, что всю механику процесса можно разложить на силы, которые складываются геометрически (векторно) или линейно, если действуют в одном направлении. Приблизительно это будет выглядеть так:

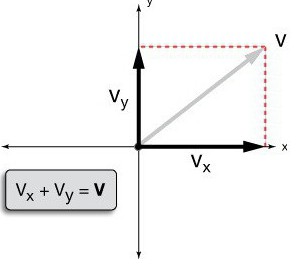
При чем же здесь равномерное движение? Все очень просто. На очень малых промежутках пути скорость движения тела вполне можно считать равномерной, с прямолинейной траекторией. Таким образом, возникла блестящая возможность изучить более сложные движения, сводя их к простым. Так изучалось равномерное движение тела по окружности.

Равномерное движение по окружности

Равномерное и равноускоренное движение можно наблюдать в перемещении планет по своим орбитам. В этом случае планета участвует в двух видах независимых движений: она равномерно перемещается по окружности и в тоже время равноускоренно движется к Солнцу. Такое сложное движение объясняется силами, действующими на планеты. Схема воздействия планетарных сил представлена на рисунке:

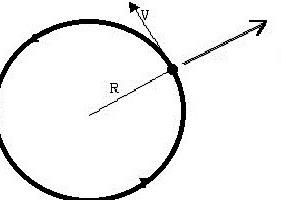
Как можно видеть, планета участвует в двух разных движениях. Геометрическое сложение скоростей и даст нам скорость планеты на данном отрезке пути.

Равномерное движение – основа для дальнейшего изучения кинематики и физики в целом. Это элементарный процесс, к которому можно свести гораздо более сложные перемещения. Но в физике, как и везде, великое начинается с малого, и запуская в безвоздушное пространство космические корабли, управляя подводными лодками, следует не забывать о тех простейших опытах, на которых Галилей когда-то проверял свои открытия.