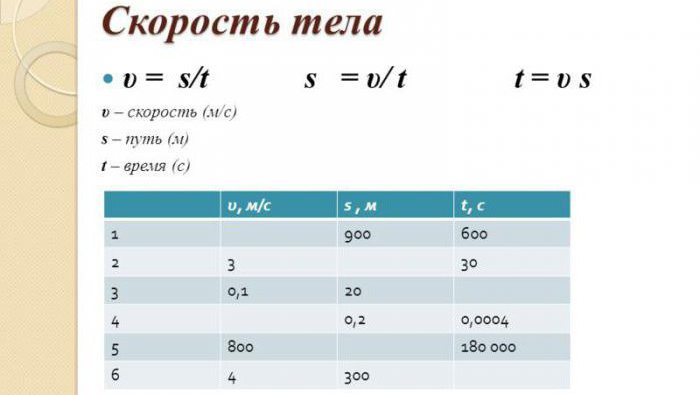
Как найти скорость. Понятие о физической величине и формула

Ввиду того что такая физическая величина, как скорость, фигурирует во многих задачах, имеющих связь с разделами механики (а именно кинематикой и динамикой), вопрос “как найти скорость” является достаточно актуальным. И эта тенденция будет сохраняться дальше, поскольку вопрос нахождения скорости (хоть она будет начальной, хоть конечной, хоть мгновенной, которая является обобщенной вариацией этих двух скоростей) останется актуальным еще надолго. А раз так, то следует узнать о скорости как физической величине все, что пригодится в последующем для решения задач.

Где упоминается скорость тела?

На самом деле, в реальном мире мы сталкиваемся со скоростью ежесекундно. Если так подумать, на Земле постоянно что-то да находится в движении. Вы можете попробовать возразить, ограничившись, например, пределами своей комнаты. То есть, по мнению некоторых людей, ночью в комнате ничего не движется. Кровати, шкафы, стулья, стол и прочие предметы находятся на своих местах, в то время как сам человек спит, то есть не движется.

Следовательно, скорость любого элемента данной системы (комнаты, как мы условились считать) равна нулю. Да, в этом что-то есть, и с одной стороны, человек, выдвинувший такое предположение, мог оказаться правым. Но не следует забывать о том, что своеобразную систему представляет собой сама наша планета Земля, а не только предметы, которые на ней находятся. А ведь все мы знаем, что ежесекундно Земля вращается вокруг своей оси. В этой системе отсчета все тела, находящиеся в пределах планеты, также совершают движение. Поэтому говорить о том, что предмет, который, казалось бы, не двигается, находится в абсолютном покое, нельзя. Это первое, что нужно было бы сказать о скорости тела.

С детской скамьи мы учимся решать много задач не только физического, но и математического характера. Их в настоящее время не так много, и ставка делается больше на гуманитарные дисциплины наподобие иностранного языка, хотя они не должны преподаваться в ущерб родному языку и техническим дисциплинам. Но речь немного не об этом. Так вот, понятие скорости тела мы можем встретить не только в задачах по физике, хотя там она встречается, пожалуй, наиболее часто. Несколько реже, но все же фигурирует скорость тела и в задачах по математике.

Наверняка все помнят эти до ужаса ненавистные (в большинстве случаев) задачи, в которых требовалось найти, через сколько времени встретятся два автомобиля, если они движутся с такими-то скоростями. Условия при этом могут быть самые разные. То движение происходит по круговой траектории (спортсмены на велосипедах или мотоциклах), то по прямолинейной траектории. В общем, задач множество. И как бы там ни было, а наша задача заключается в том, чтобы понять, что нужно делать, столкнувшись с вопросом о том, как найти скорость в том или ином случае.

Скорость в физике

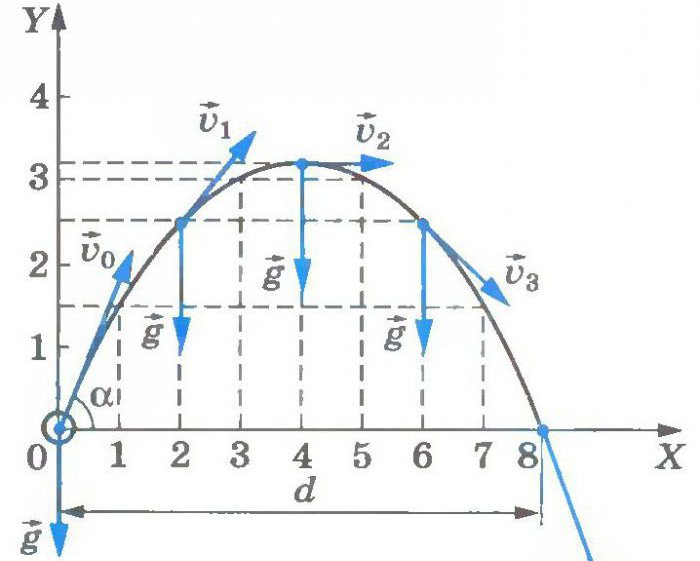
Нередко ученики, которые впервые (а возможно и повторно) знакомятся с азами (можно их так назвать) кинематики, задаются вопросом о том, как найти начальную скорость. Это действительно важно, поскольку множество задач из первой части материалов, которые предлагаются ученику для самостоятельного решения на экзамене в 9 и 11 классе, имеют целью нахождение начальной скорости либо величин, каким-либо образом связанных с ней.

Да и вообще, хотелось бы отметить, что в определенных случаях знание формул кинематики (в том числе и формулы начальной скорости при соответствующем виде движения) поможет решить даже задачу из последней части. Разумеется, на соответствующую тему. Итак, как найти начальную скорость в задачах по физике? Давайте вспомним, какие формулы даются в разделе кинематики для использования их в целях нахождения неизвестных величин.

Виды движения

Как известно, движение может быть равномерным, а может быть равноускоренным (равнозамедленным). Если из названия непонятно, каковы различия всех этих трех видов движения, то попробуем объяснить более конкретно. Равномерным движением называется движение, осуществляемое при постоянной скорости тела или материальной точки. В то же время равноускоренным движением называется движение, осуществляемое при наличии постоянного ускорения. Равнозамедленное движение – аналог равноускоренного, только ускорение при этом будет отрицательным.

На деле все выглядит так. При равномерном движении есть постоянная скорость, но ускорение отсутствует. Оно равно нулю. Тело при этом за одинаковые промежутки времени будет проходить одинаковые расстояния (если соответствующие условия не изменяются, нет никаких внешних воздействий). О каких воздействиях идет речь? На бумаге все выглядит идеально. Посмотрели на скорость, посмотрели на дистанцию, нашли время. Вот из этих трех параметров – время, скорость, расстояние – складывается своеобразный равносторонний треугольник, на котором строятся многие задачи.

Нюансы

На деле же представим, что есть два участка дороги. Один ровный, другой с небольшими бугорками. Скорость у автомобиля пускай будет та же самая, но за счет сопротивления за один и тот же промежуток времени он пройдет на втором участке дороги расстояние меньшее, чем на первом. Однако это уже задача больше из категории динамики, где рассматриваются причины, вызывающие движение тела. Кстати, логично, что при равномерном движении его конечная и начальная скорость совпадают друг с другом, а также с мгновенной скоростью.

При равноускоренном движении все будет несколько иначе. Будет присутствовать положительное ускорение, оно будет постоянным. Но вследствие присутствия ускорения скорость будет ежесекундно изменяться. В связи с этим вопрос о том, как найти скорость в определенный момент времени при наличии ускорения в системе, становится актуальным. Для этого существуют определенные формулы.

Как найти скорость?

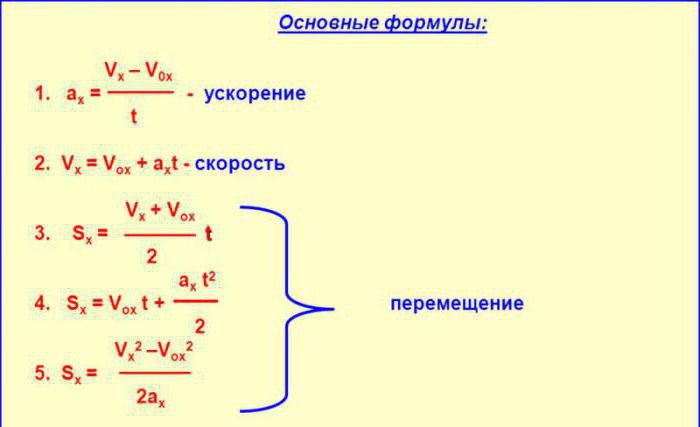
Чтобы найти скорость тела в определенный момент времени, найти начальную скорость или конечную, необходимо для начала разобраться с типом движения. Если оно равномерное, то все достаточно просто. Для того чтобы найти скорость в этом случае, следует просто поделить пройденное телом расстояние на прошедшее время. Это и будет ответ. Немного сложнее дело обстоит в том случае, если движение равноускоренное или равнозамедленное.

Допустим, что тело в течение некоторого периода времени ускоряется. Вот одна из формул, которая может быть применена к задаче подобного рода: S = V0t +(-) at^2/2. В выражении в качестве результата (левая часть уравнения) указано пройденное телом расстояние. В правой части у нас слева направо располагается начальная скорость, время, ускорение. Почему указаны два знака? Если тело разгоняется, ускорение будет положительным, перед слагаемым будет ставиться знак “плюс”. Если ускорение отрицательное, перед слагаемым будет ставиться знак “минус”.

Как найти скорость сближения?

Допустим, что у нас есть два тела, которые движутся с известными скоростями. В общем виде пускай это будет V1 и V2. Тогда скорость их сближения будет равна модулю разности. То есть V1 – V2, взятое со знаком “плюс”. Модуль берется для того, чтобы не вдаваться в векторные нюансы, то есть не работать с направлением скоростей, поскольку скорость, как и ускорение, - величина не скалярная, а векторная. Но усложнения в школьной программе ни к чему (по крайней мере, подобные), поэтому применяется модуль.