Интерполяция - это... Определение, особенности расчета и примеры интерполяции

Многие из нас сталкивались с непонятными терминами в разных науках. Но находится очень мало людей, которых не пугают непонятные слова, а наоборот, приободряют и заставляют всё больше углубиться в изучаемый предмет. Сегодня речь пойдёт о такой вещи, как интерполяция. Это способ построения графиков по известным точкам, позволяющий с минимальным количеством информации о функции предсказать её поведение на конкретных участках кривой.

Перед тем как перейти к сути самого определения и рассказать о нём подробнее, немного углубимся в историю.

История

Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.

Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.

Интерполяция представляет собой достаточно узкое понятие, поэтому её история не так богата фактами. В следующем разделе разберёмся, что такое интерполяция на самом деле и чем она отличается от своей противоположности - экстраполяции.

Что такое интерполяция?

Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.

Однако есть другие, более сложные и точные способы выполнить поставленную задачу построения графика по точкам. Итак, интерполяция - это фактически "предсказание" поведения функции на конкретном участке, ограниченном известными точками.

Существует схожее понятие, связанное с этой же областью, - экстраполяция. Она представляет собой также предсказание графика функции, но за пределами известных точек графика. При таком способе предсказание делается на основе поведения функции на известном промежутке, и потом эта функция применяется и для неизвестного промежутка. Такой способ очень удобен для практического применения и активно используется, например, в экономике для прогнозирования взлётов и падения на рынке и для предсказания демографической ситуации в стране.

Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.

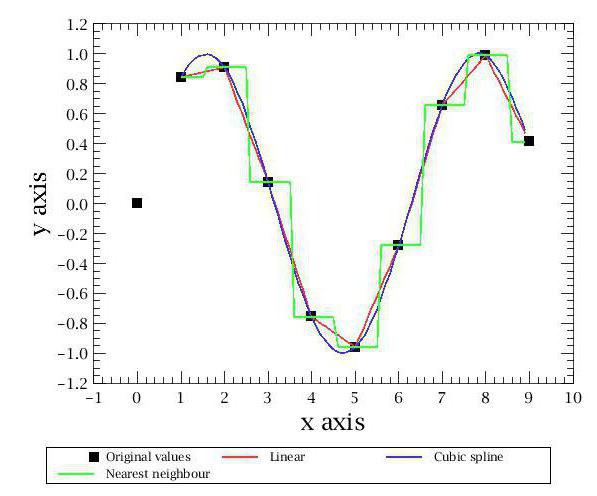
Виды интерполяции

Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.

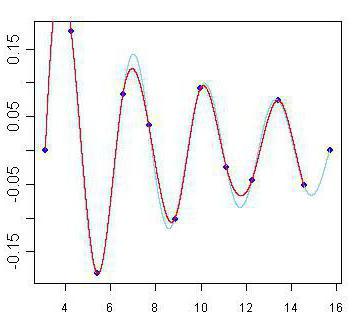
Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами. Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек. Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.

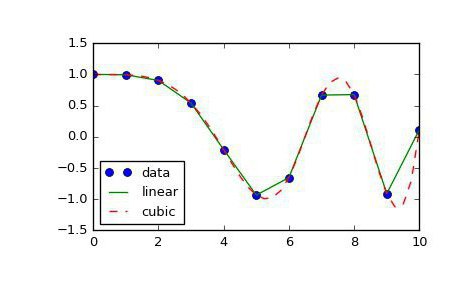
Усложнённые виды интерполяции

Есть более интересный, но при этом более сложный способ интерполяции. Его придумал французский математик Жозеф Луи Лагранж. Именно поэтому расчет интерполяции по этому методу назван его именем: интерполяция по методу Лагранжа. Фокус тут вот в чём: если способ, изложенный в предыдущем абзаце, использует для расчета только линейную функцию, то разложение методом Лагранжа предполагает также использование многочленов более высоких степеней. Но не так просто найти сами формулы интерполяции для разных функций. И чем больше точек известно, тем точнее получается формула интерполяции. Но есть и масса других методов.

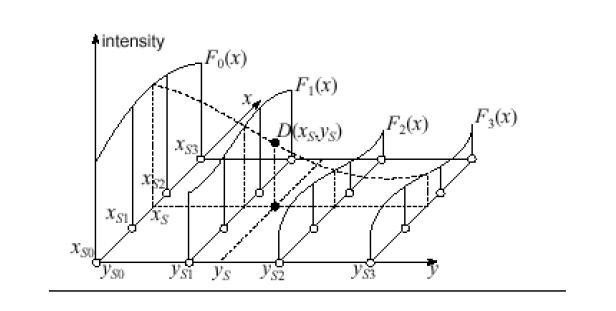
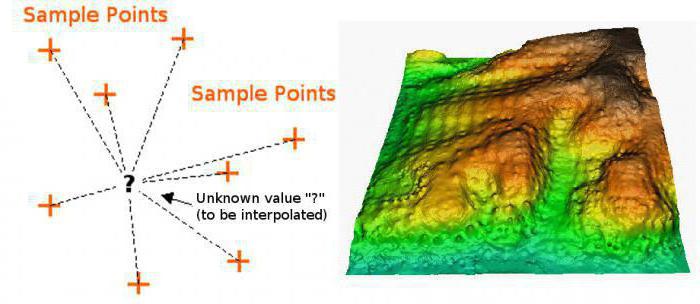
Существует и более совершенный и приближенный к реальности метод расчета. Формула интерполяции, используемая в нём, представляет собой совокупность многочленов, применение каждого из которых зависит от участка функции. Такой метод называется сплайн-функцией. Кроме того, есть ещё и способы, позволяющие провести такую вещь, как интерполяция функций двух переменных. Тут всего два метода. Среди них билинейная или двойная интерполяция. Этот способ позволяет без труда построить график по точкам в трёхмерном пространстве. Другие методы затрагивать не будем. Вообще, интерполяция - это универсальное называние для всех этих способов построения графиков, но многообразие способов, которыми можно осуществить это действие, заставляет делить их на группы в зависимости от вида функции, которая подлежит этому действию. То есть интерполяция, пример которой мы рассмотрели выше, относится к прямым способам. Есть также обратная интерполяция, которая отличается тем, что позволяет вычислить не прямую, а обратную функцию (то есть x от y). Рассматривать последние варианты мы не будем, так как это достаточно сложно и требует хорошей математической базы знаний.

Перейдём к, пожалуй, одному из важнейших разделов. Из него мы узнаем, как и где обсуждаемая нами совокупность методов применяется в жизни.

Применение

Математика, как известно, царица наук. Поэтому даже если вы сначала не видите смысла в тех или иных операциях, это не значит, что они бесполезны. Вот, например, кажется, что интерполяция - это бесполезная вещь, с помощью которой только графики строить можно, которые сейчас мало кому нужны. Однако при любых расчётах в технике, физике и многих других науках (например, биологии), крайне важно представлять достаточно полную картину о явлении, имея при этом определённый набор значений. Сами значения, разбросанные по графику, не всегда дают чёткие представления о поведении функции на конкретном участке, значениях её производных и точек пересечения с осями. А это очень важно для многих областей нашей с вами жизни.

А как это пригодится в жизни?

На подобный вопрос бывает очень сложно ответить. Но ответ прост: никак. Именно эти знания вам никак не пригодятся. А вот если вы поймёте этот материал и методы, с помощью которых осуществляются эти действия, вы потренируете свою логику, которая в жизни очень пригодится. Главное - не сами знания, а те навыки, которые человек приобретает в процессе изучения. Ведь недаром существует поговорка: "Век живи - век учись".

Смежные понятия

Вы можете сами понять, насколько важна была (и до сих пор не теряет свою важность) эта область математики, взглянув на многообразие других концепций, связанных с данной. Мы уже говорили об экстраполяции, но есть ещё и аппроксимация. Может быть, вы уже слышали это слово. В любом случае то, что оно обозначает, мы тоже разбирали в этой статье. Аппроксимация, как и интерполяция, - это понятия, связанные с построением графиков функций. Но отличие первой от второй в том, что она представляет собой приблизительное построение графика на основе сходных известных графиков. Эти два понятия очень похожи между собой, и тем интереснее изучать каждое из них.

Заключение

Математика - не такая сложная наука, как кажется на первый взгляд. Она, скорее, интересная. И в этой статье мы попытались вам это доказать. Мы рассмотрели понятия, связанные с построением графиков, узнали, что такое двойная интерполяция, и разобрали на примерах, где она применяется.