Распределительный закон умножения относительно сложения

Математики - ленивые люди, поэтому они всё время создавали какие-то формулы, законы, обозначения. Их старания не прошли зря, теперь современный человек может легко решать уравнения и задачи. С лёгкостью доказывать теоремы по геометрии, и всё это благодаря формулам, обозначениям, свойствам!

Законы умножения и сложения

Их для умножения и сложения чисел всего три. Они очень полезны, благодаря им можно с лёгкостью решать большие уравнения. Каждый из них имеет свою формулу и название.

Первый закон умножения и сложения - сочетательный. Числа в таком случае группируют, зная, что сумма и произведение все равно не изменятся.

Второй закон умножения и сложения - переместительный. В этом случае числа перемещают так, как будет удобно, зная, что сумма и произведение также останутся теми же.

Третий, наиболее часто используемый, - распределительный закон. Его смысл в том, чтобы выполнять действия не отдельно для каждого числа, а умножать сразу на сумму. И наоборот, вносить множитель в скобки, умножая на каждое слагаемое. Это действительно удобно, и стоит научиться использовать этот закон!

Эти законы нельзя использовать для деления и вычитания, так как они могут изменить конечный результат.

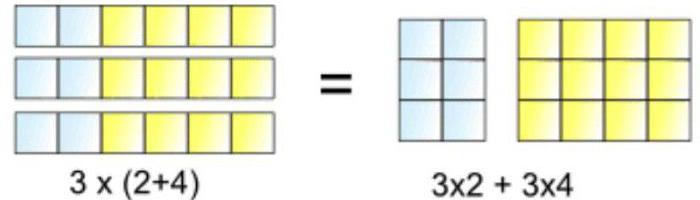
Распределительный закон

Он очень удобен, ведь с его помощью можно умножать число на сумму без каких-либо трудностей! А всё потому, что распределять намного удобнее, чем просто умножать на каждый множитель.

Для наглядности можно рассмотреть пример, где он применяется при умножении и сложении.

Дано выражение: 3 х 2 + 3 х 5.

Так выглядит обычное выражение. Если мы будем использовать распределительный закон, оно будет выглядеть так: 3 х (2 + 3) = 3 х 5 = 15.

Как видим, пользуясь этим удобным "средством", можно намного быстрее решать различные уравнения!

Всё на свете имеет своё название и формулировку, распределительный закон - не исключение! Стоит заучить его формулировку, чтобы с лёгкостью пользоваться им в любых условиях и при любых обстоятельствах. Стоит понять его действие!

Пример, где применяется распределительный закон умножения относительно сложения

Рассмотрим ещё один пример, где применим этот закон: 2 х 5 + 2 х 3 = 16.

Такое выражение было первоначально, а потом оно стало таким: 2 х (5 + 3) = 2 х 8 = 16.

Как видим, ответ не изменился, а выполнять действия стало намного легче! Это же прекрасно! Мы смогли облегчить себе жизнь!

Распределительный закон умножения относительно сложения очень полезен, поэтому им нужно пользоваться! Не стоит бояться пробовать что-то новое! Все свойства, теоремы и формулы есть в математике неспроста!