Логическое выражение: построение и упрощение

Главная задача логики – выяснить, является ли некоторое утверждение ложным или его можно считать истинным. Для этого было изобретено несколько методов. Разработаны способы определения того, истина это или ложь, на основе других высказываний и их атрибутов. Логическое выражение – базовое понятие науки, и его параметры определяют, какие операции могут быть совершены.

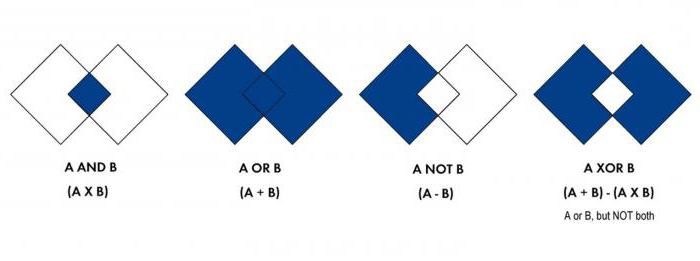
Общие термины

Сегодня логика изучается в форме математической логики. В ее основе исключительно формальные методы познания. Один из ключевых разделов направления – алгебра логики. Она специализируется только на сложных объектах и методах, позволяющих установить их параметры. Используются строго алгебраические способы изучения.

Наука называется алгеброй Буля, так как автором ее является Джордж Буль, сформулировавший свои основные идеи в 1854 году, когда он выпустил фундаментальную книгу. Буль поставил перед собой задание изучить операции, на основании которых функционирует человеческий ум, понять, каков механизм рассуждений, описать его символами. Добившись в этом успеха, он сумел создать новую науку.

Логические выражения в программировании

Условное логическое выражение представляет собой некоторые переменные и постоянные, которые классифицируются простыми. Все объекты объединены между собой сравнением. В результате вычисления удается получить некоторое конечное условное выражение: истина либо ложь.

Наиболее применима логика в программировании. На примере языка Паскаль можно выделить наиболее важные операции, используемые на практике:

• определение большего из двух;
• определение меньшего из двух;
• вычисление меньшего либо равного;
• вычисление большего либо равного;
• определение равенства двух выражений;
• заключение, что выражения не равны между собой.

Если при программировании необходимо построить логическое выражение, но сравниваются между собой вещественные числа, учтен должен быть следующий факт: представление чисел неточно, так как обязательно происходит округление. Это означает, что операция вычисления строгого равенства не может быть точной. Опытные программисты рекомендуют по возможности избегать обращаться к этой операции, поскольку велика вероятность, что равенство в итоге будет посчитано как ложное, не являясь таковым.

Пример: x = (2.23*x/2.23)

Согласитесь, визуально видна истинность формулы. Но при записи ее в компьютерный код и неизбежности погрешности округления при расчетах она окажется ложной.

Еще один тонкий момент: условное логическое выражение обязательно записывается в скобках, если оно является операндом. Правило следует из разработанной иерархии операций. Например, сравнение по своему приоритету ниже прочих, а логических операции – высокий. Чтобы изменить относительно такого порядка процесс расчета конкретного примера, придется расставить скобки.

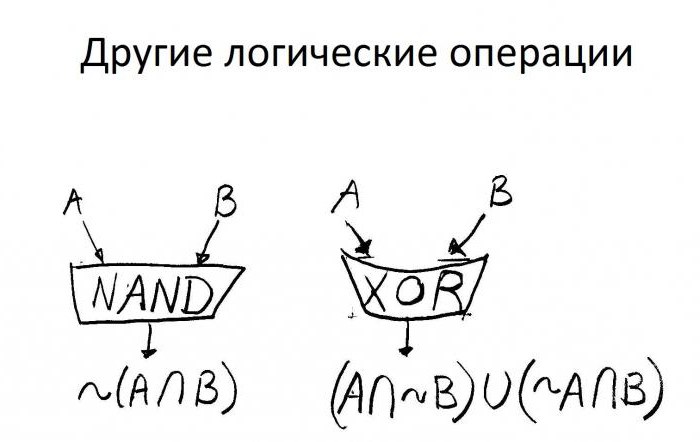
Основа науки

Под объектом в логике принято понимать такое повествование, о котором точно сообщают, что оно является ложью, истиной. Значение логического выражения, когда оно истинно, записывают единицей, второй вариант обозначается нулем.

Под логическими операциями принято понимать такие действия (как правило, мыслительный процесс), которые в итоге дают увеличение знаний, а также ведут к формированию совершенно новых объектов.

Логическое выражение бывает устным, можно его записать. Оно включается в объекты наряду с константами. Выражение напрямую зависит от переменных объектов, становясь либо единицей, либо нулем.

Если пришлось столкнуться со сложным высказыванием, нужно помнить, что оно включает в себя сложные простые выражения, для соединения которых применялись логические операции.

Логика выделяет ключевые операции, именуемые:

• конъюнкция;
• эквивалентность;
• дизъюнкция;
• импликация;
• инверсия.

Для решения практически любого примера их будет достаточно.

Конъюнкция

Под этим термином принято понимать такую сложную операцию, которая может быть истиной, лишь если оба простых составляющих являются истиной. Прочие варианты считаются ложными.

Записывается так: F = А & В.

Таблица:

Дизъюнкция

В этой ситуации истинность логических выражений определяется, исходя из анализа значения (единица и ноль) составляющих простых выражений. Если оба они ложны, то функция также имеет значение «ноль». В противном случае ее значение равняется единице.

Записывается так: F = A + B.

Таблица:

Инверсия

Термин обозначает операцию, когда происходит превращение в ложное выражение, прежде бывшего истинным, и наоборот. Если исходный объект верный, в результате получаем ложный, а если изначально была ложь, она трансформируется в истину.

Таблица:

Равнозначность

Это логическое выражение лишь в том случае будет значить единицу, когда оба выражения в примере значат одно и то же.

Таблица:

Импликация

Термин применяется к такому сложному выражению логики, которое ложно, если из истины следует ложь. Прочие ситуации: значение равняется единице. Операция применяется для двух простых объектов, из которых одно называют условием, а другое – следствием.

Таблица:

Операции: логические нюансы

Зная, какое логическое выражение используется в качестве объекта, можно правильно вычислить результат. При этом следует помнить, что операции в логике – это как в арифметике те операции, которые необходимы для взаимодействия с числами. Логические операции помогают строить логически выражения – это также является параллелью с алгеброй.

В составе логических выражений встречаются константы и переменные. Первые имеют конкретное значение – ноль либо единицу. В случае если выражение в себя включает некоторые переменные, оно тем самым будет задавать булеву функцию, чье значение вычисляется на основании аргументов. Значения аргументов для каждой задачи указаны в условиях. Необходимо просто подставить их в выражение, после чего вести дальнейший расчёт.

Любое логическое выражение может иметь собственную таблицу истинности, то есть объект, детально во всех вариациях описывающий, какие значения и когда принимает функция, если использован конкретный набор переменных. Одна строчка такой таблицы – один набор исходных условий для вычисления. Если в функции задействовано N переменных, то строк вдвое больше.

Таблицы истинности

Выделяют следующие общие свойства, характерные всякой таблице:

• уже упомянутое число строк, вдвое превышающее количество переменных;
• число столбцов таблицы на один превышает количество задействованных переменных.

Вне зависимости от того, каково множество значений переменных, заданное в условии, всегда можно сформулировать такое выражение, которое будет равняться единице на определенном наборе переменных.

Записывается это как «дизъюнкция конъюнкций». На практике это означает, что можно построить некоторое выражение, имея перед собой готовую таблицу истинности. Конечно, объемы этой таблицы могут существенно усложнить задачу математика.

Упрощения

Нередко бывают ситуации, когда математическое выражение требует для адекватности решения упрощения. Есть определенные преобразования, применимые в булевой логике.

В частности, одно выражение можно заменить на другое, являющееся эквивалентным. Проверяют эквивалентность, анализируя таблицы истинности. Если они совпадают, можно проводить замену. Здесь вступает в действие правило подставной, когда в объекте А меняется на некоторое подвыражение Р, присутствовавшее здесь ранее Q, и получается выражение В. По всем расчетам оно эквивалентно А.

Упрощение логических выражений принято именовать минимизацией. Главная задача минимизации – это представить функцию в таком виде, когда букв, операций имеется наименьшее число из возможных. Добиться желаемого можно одним из двух вариантов:

• алгебраическим;
• графическим.

Алгебраический метод

Упростить логическое выражение алгебраическим методом можно, упростив формулу. Это производится уже описанными выше эквивалентными преобразованиями. При этом необходимо учитывать тождества и правила, существующие в булевой алгебре.

Упрощенное выражение от того, которое необходимо было решить изначально, отличается в первую очередь количеством букв. Впрочем, нередки задачи, когда приходится доказывать эквивалентность исходного выражения и полученного в результате упрощения. Производится это сличением таблиц истинности.

Если в примере представлены элементарные высказывания, можно добиться их видоизменения, прибегая не только к общим правилам, но и к тем, что связаны с операциями над множествами.

При анализе высказывания, связанного со множествами, нередко оптимальный вариант – сводить выражения до импликации, когда члены уже не содержат импликации.