Четыре формулы, по которым можно вычислить площадь ромба. Свойства ромба

Ромб – это особая фигура в геометрии. Благодаря его особым свойствам, существует не одна, а несколько формул, с помощью которых вычисляется площадь ромба. Что это за свойства и какие наиболее распространенные формулы для поиска площади этой фигуры существуют? Давайте разберемся.

Какая геометрическая фигура называется ромбом

Прежде чем выяснить, чему равна площадь ромба, стоит узнать, что же это за фигура.

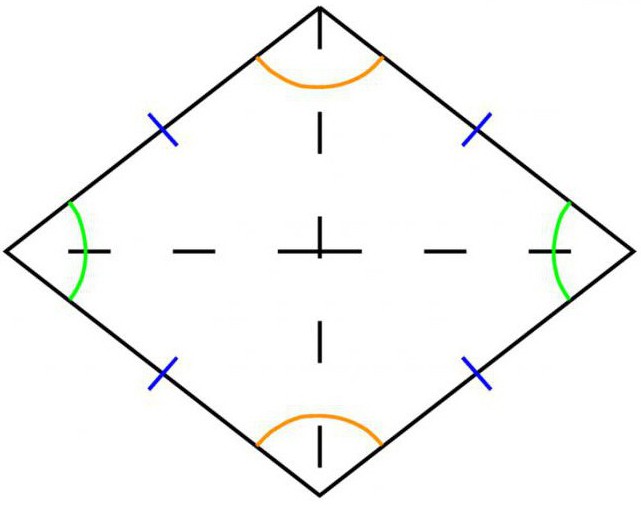
Ромбом со времен Евклидовой геометрии называется симметричный четырехугольник, все четыре стороны коего являются равными между собою по длине и попарно параллельными.

Происхождение термина

Название этой фигуры пришло в большинство современных языков из греческого, через посредничество латыни. «Прародителем» слова «ромб», стало греческое существительное ῥόμβος (бубен). Хотя жителям двадцатого века, привыкшим к круглым бубнам, тяжело представить их другой формы, но у эллинов эти музыкальные инструменты традиционно изготавливались не круглой, а ромбовидной формы.

В большинстве современных языков данный математический термин употребляется, как и в латыни: rombus. Однако в английском языке иногда ромбы называют diamond (алмаз или диамант). Такое прозвище данная фигура получила из-за своей особой формы, напоминающей драгоценный камень. Как правило, подобный термин используют не для всех ромбов, а только для тех, у которых угол пересечения его двух сторон равен шестидесяти или сорока пяти градусам.

Впервые эта фигура была упомянута в трудах греческого математика, жившего в первом веке новой эры - Герона Александрийского.

Какими свойствами обладает эта геометрическая фигура

Чтобы найти площадь ромба, в первую очередь нужно знать, какими особенностями обладает данная геометрическая фигура.

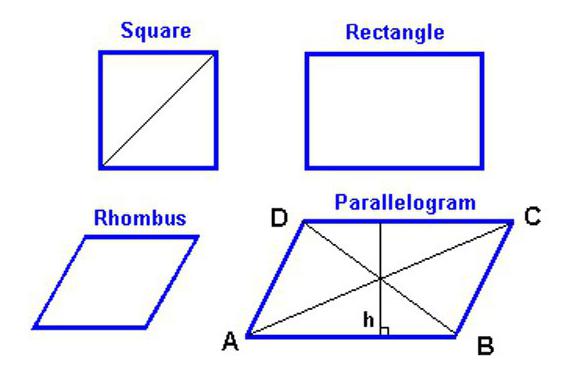
• Как уже было сказано в определении ромба, он является четырехугольником. А по той причине, что его противоположные стороны попарно являются параллельными между собою, ромб также может именоваться параллелограммом, а значит, на него распространяется большинство свойств этой фигуры.
• Обе диагонали ромба в точке своего пересечения равномерно делятся надвое. А из-за того, что пересекаются они под углом в девяносто градусов, диагонали делят фигуру на 4 треугольника прямоугольных.
• В любом ромбе диагонали делят его углы надвое, являясь одновременно их биссектрисами.
• Если каждую из двух диагоналей ромба возвести в степень квадрата, то их сумма будет равна произведению квадрата стороны этой фигуры и числа четыре.
• Если соединить линиями средины четырех сторон ромба, полученная фигура окажется прямоугольником.
• Если в ромб (независимо от его углов) вписана окружность, тогда ее центральная точка совпадет с центром пересечения диагоналей.
• Диагонали в ромбе соприкасаются с осями его симметрии под углами девяносто градусов.
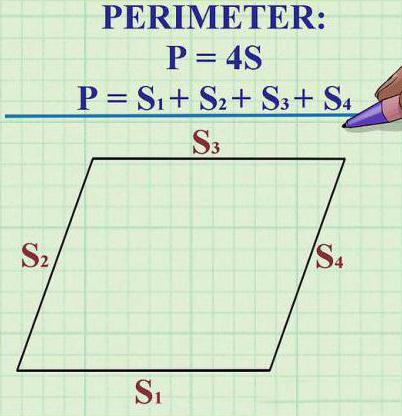
• Поскольку все стороны ромба идентичны между собою по длине, его периметр вычисляется по формуле Р=4 х К (К - это длинна одной из сторон).
  

При каких условиях параллелограмм является ромбом

Как известно, каждый ромб является параллелограммом, но при этом не всякий параллелограмм – это ромб. Чтобы точно утверждать, что представленная фигура действительно является ромбом, а не простым параллелограммом, она должна соответствовать одному из трех основных признаков, выделяющих ромб. Или всем трем сразу.

1. Диагонали параллелограмма пересекаются под углом девяносто градусов.
2. Диагонали разделяют углы надвое, выступая в качестве их биссектрис.
3. Не только параллельные, но и смежные стороны имеют одинаковую длину. В этом, кстати, одно из основных различий между ромбом и параллелограммом, поскольку у второй фигуры одинаковы по длине лишь параллельные стороны, но не смежные.

При каких условиях ромб является квадратом

По своим свойствам в отдельных случаях ромб одновременно может становиться квадратом. Чтобы наглядно подтвердить это утверждение, достаточно просто повернуть квадрат в любую сторону на сорок пять градусов. Получившаяся фигура окажется ромбом, каждый из углов которого равен девяноста градусам.

Также, чтобы подтвердить, что квадрат является ромбом, можно сопоставить признаки этих фигур: в обоих случаях все стороны равны, а диагонали являются биссектрисами и пересекаются под углом в девяносто градусов.

Как узнать площадь ромба с помощью его диагоналей

В современном мире в интернете можно найти практически все материалы для выполнения необходимых расчетов. Так, существует масса ресурсов, оснащенных программами для автоматического вычисления площади той или иной фигуры. Причем, если (как в случае с ромбом) есть несколько формул для этого, то есть возможность выбирать, какой из них удобнее всего будет воспользоваться. Однако, прежде всего, необходимо самим уметь вычислять площадь ромба без помощи компьютера и ориентироваться в формулах. Для ромба их существует немало, но самые известные из них четыре.

Одним из самых простых и распространенных способов узнать площадь этой фигуры, если есть информация о длине его диагоналей. Если в задаче есть эти данные, в таком случаем можно применить следующую формулу для нахождения площади: S = КМ x LN/2 (КМ и LN – это диагонали ромба KLMN).

Можно проверить достоверность этой формулы на практике. Допустим, у ромба KLMN длина одной его диагонали КМ – 10 см, а второй LN – 8 см. Тогда подставляем эти данные в указанную выше формулу, и получаем следующий результат: S = 10 х 8/ 2= 40 см².

Формула для вычисления площади параллелограмма

Существует и другая формула. Как было указано выше в определении ромба, он является не просто четырехугольником, но и параллелограммом, и обладает всеми особенностями данной фигуры. В таком случае для нахождения ее площади вполне целесообразно использовать формулу, применяемую для параллелограмма: S = KL х Z. В данной случае KL – это длинна стороны параллелограмма (ромба), а Z – это длинна высоты, проведенной к данной стороне.

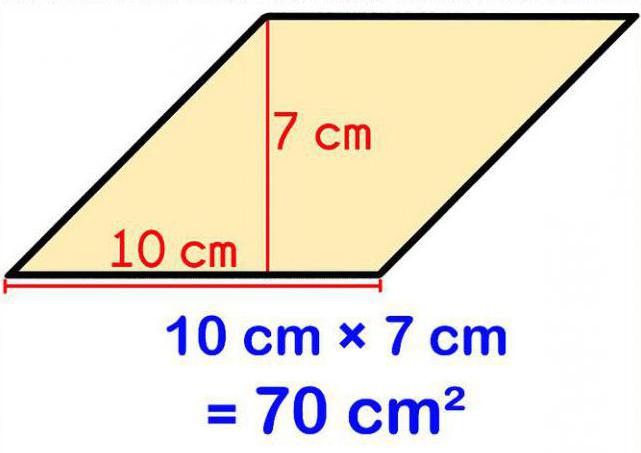
В отдельных задачах длина стороны не предоставлена, зато известен периметр ромба. Поскольку выше была указана формула его нахождения, с ее помощью можно узнать и длину стороны. Итак, периметр фигуры - 10 см. Длину стороны можно узнать, инвертировав формулу периметра и разделив 10 на 4. Результатом окажется 2,5 см - это и есть искомая длина стороны ромба.

Теперь стоит попробовать подставить это число в формулу, зная, что длинна высоты, проведенной к стороне, также равна 2,5 см. Теперь попробуем поставить эти значения в вышеупомянутую формулу площади параллелограмма. Получается, что площадь ромба равна S = 2,5 х 2,5 = 6,25 см².

Другие способы вычисления площади ромба

Те, кто уже освоили синусы и косинусы, могут использовать для нахождения площади ромба формулы, содержащие их. Классическим примером служит следующая формула: S = КМ² х Sin KLM. В данном случае площадь фигуры равна произведению двух сторон ромба, умноженному на синус угла между ними. А поскольку в ромбе все стороны одинаковы, то проще сразу произвести одну сторону в квадрат, как и было показано в формуле.

Проверяем на практике данную схему, причем не просто к ромбу, а к квадрату, у которого, как известно, все углы прямые, а значит, равны девяносто градусам. Допустим, одна из сторон равна 15 см. Также известно, что синус угла в 90° равен единице. Тогда, согласно формуле, S = 15 х 15 х Sin 90°= 255х1=255 см^2.

Помимо вышеперечисленных, в отдельных случаях используется еще одна формула, с использованием синуса для определения площади ромба: S = 4 х R²/Sin KLM. В данном варианте используется радиус вписанной в ромб окружности. Он возносится в степень квадрата и умножается на четыре. А весь результат делиться на синус угла, близлежащего к вписанной фигуре.

В качестве примера для простоты вычислений возьмем опять квадрат (синус его угла будет всегда равен единице). Радиус вписанного в него круга – 4,4 см. Тогда площадь ромба будет вычисляться так: S= 4 х 4,4²/ Sin 90 °= 77,44 см²

Приведенные выше формулы нахождения радиуса ромба - далеко не единственные в своем роде, однако они являются наиболее простыми для понимания и проведения вычислений.