Признаки, составляющие элементы и свойства равнобедренного треугольника

Первые историки нашей цивилизации – древние греки - упоминают Египет как место зарождения геометрии. Трудно с ними не согласиться, зная, с какой потрясающей точностью возведены гигантские усыпальницы фараонов. Взаимное расположение плоскостей пирамид, их пропорции, ориентация по сторонам света – достичь такого совершенства было бы немыслимо, не зная основ геометрии.

Само слово "геометрия" можно перевести как «измерение земли». Причём слово «земля» выступает не как планета – часть Солнечной системы, а как плоскость. Разметка площадей под ведение сельского хозяйства, скорее всего, и является самой изначальной основой науки о геометрических фигурах, их видах и свойствах.

Треугольник – самая простая пространственная фигура планиметрии, содержащая всего три точки - вершины (меньше не бывает). Основа основ, может быть, оттого и мерещится в нём нечто таинственное и древнее. Всевидящее око внутри треугольника – один из самых ранних из известных оккультных знаков, причём география его распространения и временные рамки просто поражают воображение. От древних египетской, шумерской, ацтекской и других цивилизаций до более современных сообществ любителей оккультизма, разбросанных по всему земному шару.

Какими бывают треугольники

Обычный разносторонний треугольник – это замкнутая геометрическая фигура, состоящая из трёх отрезков разной длины и трёх углов, ни один из которых не является прямым. Кроме него, различают несколько особых видов.

Треугольник остроугольный имеет все углы величиной менее 90 градусов. Иными словами – все углы такого треугольника острые.

Прямоугольный треугольник, над которым во все времена плакали школьники из-за обилия теорем, имеет один угол с величиной 90 градусов или, как его ещё называют, прямой.

Тупоугольный треугольник отличается тем, что один из его углов тупой, то есть величина его - более 90 градусов.

Равносторонний треугольник имеет три стороны одинаковой длины. У такой фигуры равны также все углы.

И наконец, у равнобедренного треугольника из трёх сторон две равны между собой.

Отличительные особенности

Свойства равнобедренного треугольника определяют и его основное, главное, отличие – равенство двух сторон. Эти равные друг другу стороны принято называть бёдрами (или, чаще, боковыми сторонами), ну а третья сторона носит название «основание».

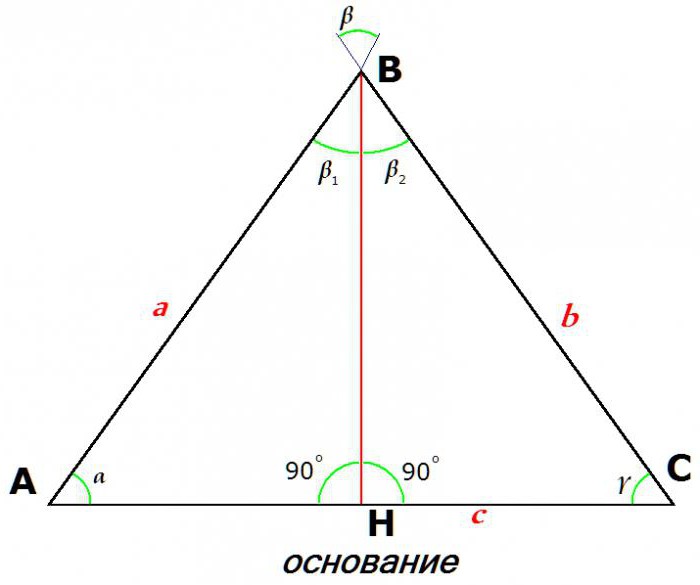
На рассматриваемом рисунке a = b.

Второй признак равнобедренного треугольника вытекает из теоремы синусов. Так как равны стороны a и b, равны и синусы их противолежащих углов:

a/sin γ = b/sin α, откуда имеем: sin γ = sin α.

Из равенства синусов следует равенство углов: γ = α.

Итак, вторым признаком равнобедренного треугольника является равенство двух углов, прилежащих к основанию.

Третий признак. В треугольнике различают такие элементы, как высота, биссектриса и медиана.

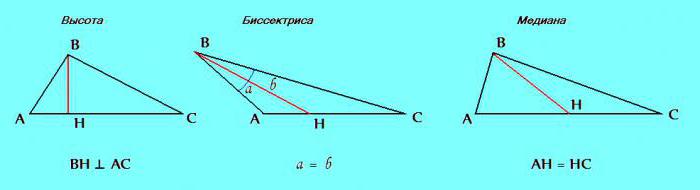
Если в процессе решения задачи выясняется, что в рассматриваемом треугольнике два любых из этих элементов совпадают: высота с биссектрисой; биссектриса с медианой; медиана с высотой - однозначно можно делать вывод, что треугольник равнобедренный.

Геометрические свойства фигуры

1. Свойства равнобедренного треугольника. Одним из отличительных качеств фигуры является равенство углов, прилежащих к основанию:

α = γ;

<ВАС = <ВСА.

2. Ещё одно свойство рассмотрено выше: медиана, биссектриса и высота в равнобедренном треугольнике совпадают, если они построены от его вершины к основанию.

3. Равенство биссектрис, проведённых из вершин при основании:

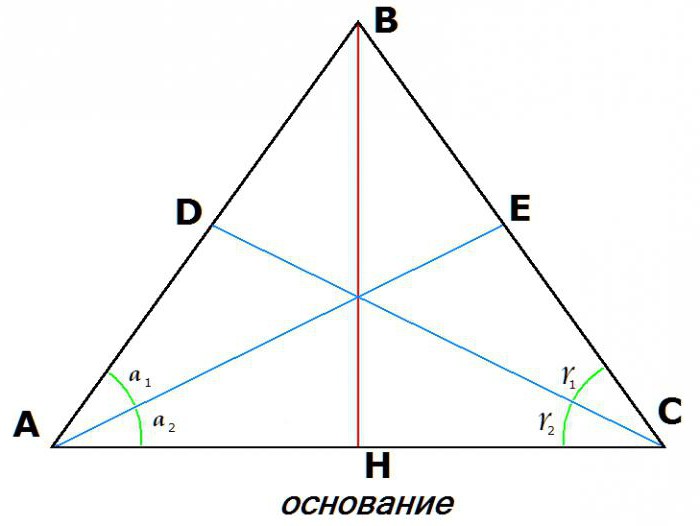
Если АЕ – биссектриса угла ВАС, а CD – биссектриса угла BCA, то: AE = DC.

4. Свойства равнобедренного треугольника предусматривают также равенство высот, которые проведены из вершин при основании.

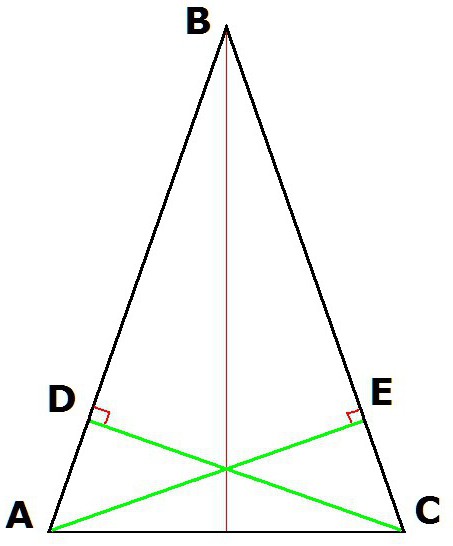
Если построить высоты треугольника АВС (где АВ = ВС) из вершин А и С, то полученные отрезки CD и АЕ будут равны.

5. Равными также окажутся и медианы, проведённые из углов при основании.

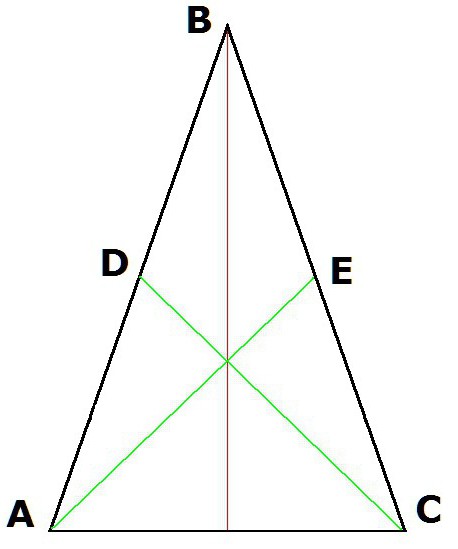
Так, если АЕ и DC – медианы, то есть AD = DB, а BE = EC, то АЕ = DC.

Высота равнобедренного треугольника

Равенство боковых сторон и углов при них привносит некоторые особенности в вычисление длин элементов рассматриваемой фигуры.

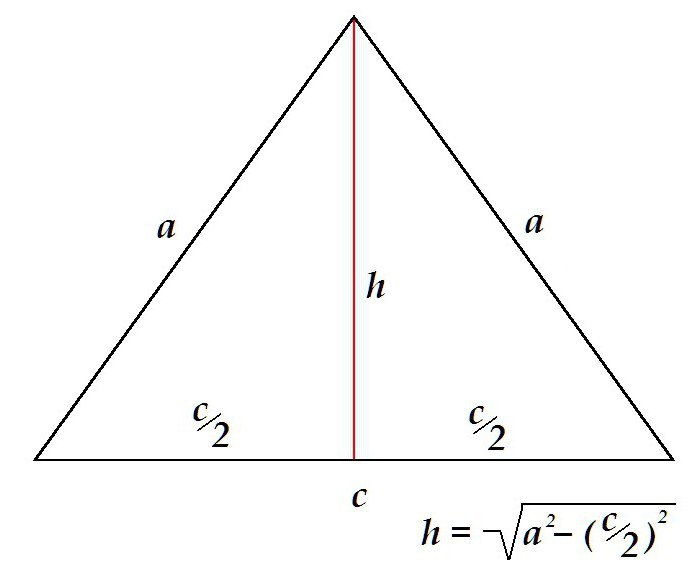
Высота в равнобедренном треугольнике делит фигуру на 2 симметричных прямоугольных треугольника, гипотенузами у которых выступают боковые стороны. Высота в таком случае определяется согласно теореме Пифагора, как катет.

У треугольника могут быть равными все три стороны, тогда он будет называться равносторонним. Высота в равностороннем треугольнике определяется аналогично, только для расчётов достаточно знать всего одно значение – длину стороны этого треугольника.

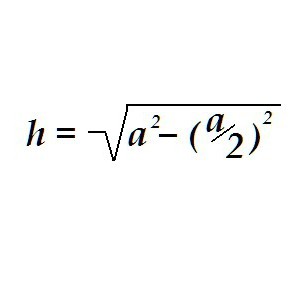
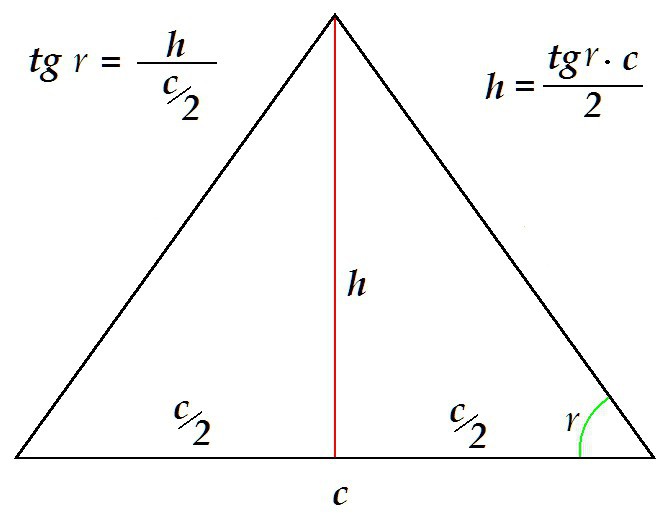
Можно определить высоту и другим путём, например зная основание и прилегающий к нему угол.

Медиана равнобедренного треугольника

Рассматриваемый тип треугольника, благодаря геометрическим особенностям, решается довольно просто по минимальному набору исходных данных. Так как медиана в равнобедренном треугольнике равна и его высоте, и его биссектрисе, то алгоритм её определения ничем не отличается от порядка вычисления данных элементов.

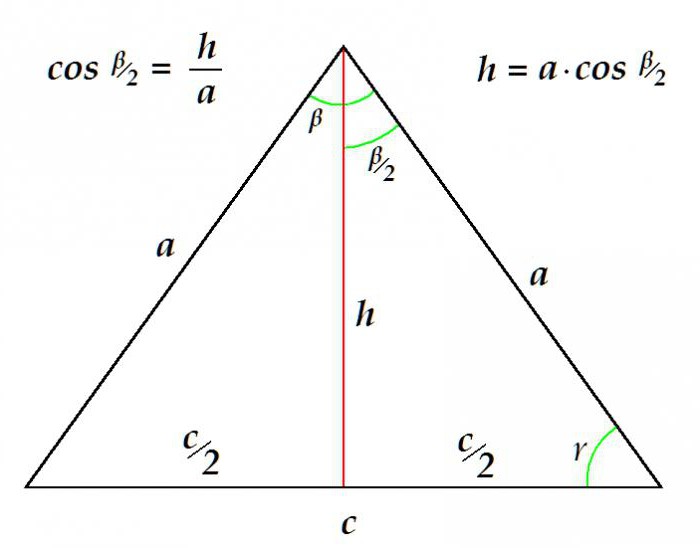
К примеру, определить длину медианы можно по известной боковой стороне и величине угла при вершине.

Как определить периметр

Так как у рассматриваемой планиметрической фигуры две стороны всегда равны, то для определения периметра достаточно знать длину основания и длину одной из сторон.

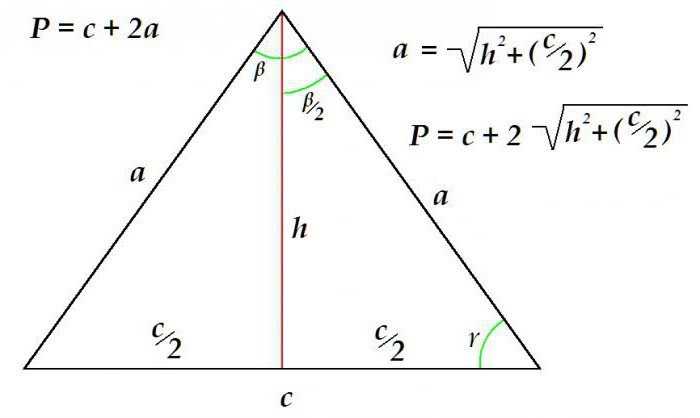
Рассмотрим пример, когда нужно определить периметр треугольника по известным основанию и высоте.

Периметр равен сумме основания и удвоенной длины боковой стороны. Боковая сторона, в свою очередь, определяется с помощью теоремы Пифагора как гипотенуза прямоугольного треугольника. Длина её равна корню квадратному из суммы квадрата высоты и квадрата половины основания.

Площадь равнобедренного треугольника

Не вызывает, как правило, трудностей и вычисление площади равнобедренного треугольника. Универсальное правило определения площади треугольника как половины произведения основания на его высоту применимо, конечно же, и в нашем случае. Однако свойства равнобедренного треугольника вновь облегчают задачу.

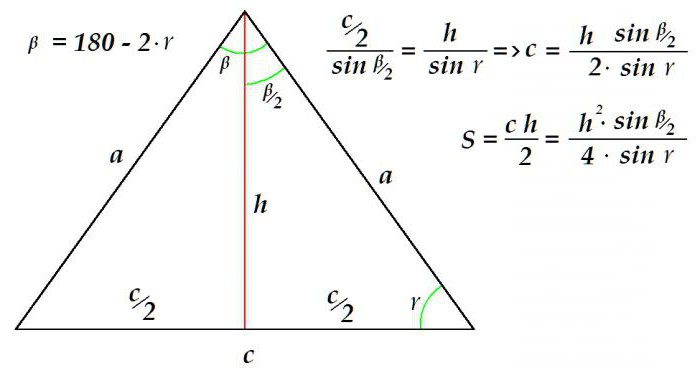
Допустим, что известны высота и угол, прилежащий к основанию. Необходимо определить площадь фигуры. Сделать это можно таким способом.

Так как сумма углов любого треугольника равна 180°, то определить величину угла не составит труда. Далее, воспользовавшись пропорцией, составленной согласно теореме синусов, определяется длина основания треугольника. Все, основание и высота – достаточные данные для определения площади - имеются.

Другие свойства равнобедренного треугольника

Положение центра окружности, описанной вокруг равнобедренного треугольника, зависит от величины угла вершины. Так, если равнобедренный треугольник остроугольный, центр круга располагается внутри фигуры.

Центр окружности, которая описана вокруг тупоугольного равнобедренного треугольника, лежит вне его. И, наконец, если величина угла при вершине равна 90°, центр лежит ровно на середине основания, а через само основание проходит диаметр окружности.

Для того чтобы определить радиус окружности, описанной около равнобедренного треугольника, достаточно разделить длину боковой стороны на удвоенный косинус половины величины угла при вершине.