Теорема и формула Остроградского - Гаусса

М.В. Остроградский - российский математик и физик времен Российской империи, академик. Внес огромный вклад в развитие математического анализа, теории вероятностей, механики (раздела физики), теории чисел. В 1826 году вывел формулу, называемую сейчас формулой Остроградского - Гаусса.

История открытия

Впервые формула Остроградского - Гаусса была упомянута Жозефом Лагранжем в 1762 году.

Далее основной способ приведения тройного интеграла к поверхностному был доказан Карлом Гауссом , который использовал в качестве основы для доказательства решение проблем в электродинамике. Произошло это в первой половине XIX века.

Далее формула в общем виде была представлена Михаилом Остроградским. С ее помощью стало возможно выразить значение дифференциала по параметру от N-кратного интеграла.

Смысл формулы Остроградского

Формула Остроградского-Гаусса соотносит тройной интеграл по пространственному объему с интегралом по поверхности на его грани. Она является аналогом формулы Грина, которая соотносит двойной интеграл по плоскости с криволинейным по ее границам.

Вывод формулы

Формула Остроградского - Гаусса: вывод. Допустим, что в области W определена подынтегральная функция R (x, y, z), которая является определенной и непрерывной. Аналогичной является и ее производная во всей области W, включая ее границу. В таком виде известна сейчас теорема Остроградского - Гаусса (формула приведена ниже).

Причем S - поверхность, которая ограничивает тело, а интеграл справа распространен на ее внешнюю сторону.

И абсолютно верно,

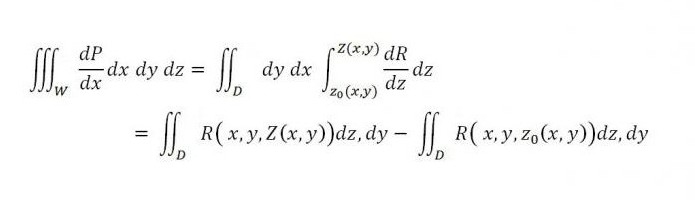
Если аналогично брать во внимание и интегралы по поверхности, то

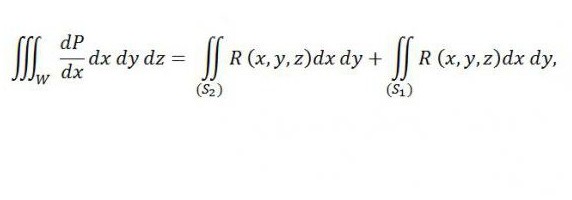
при этом справа находится сумма двух интегралов - первый из них соотносится с верхней частью поверхности (S₂), а второй - с нижней частью поверхности (S₁). Если приписать к данному равенству справа интеграл, указанный ниже, то его справедливость не будет нарушена:

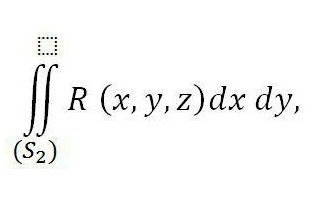
Он соотносится с внешней частью поверхности S₃ по причине равенства нулю.

Если объединить все три вышеуказанных интеграла в один, будет получен частный случай формулы Остроградского.

Несложно осознать, что данная формула верна для более широкого класса тел и справедлива так же для фигур, ограниченных абсолютно любыми нелинейными поверхностями.

Аналогично справедливы и следующие формулы:

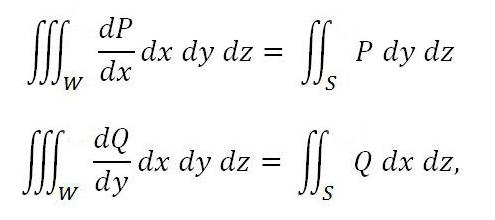
если функции Q и P непрерывны в области вместе со своими производными dP/dx и dQ/dy.

Если сложить оба равенства, будет получено выражение формулы Остроградского. Она отображает интеграл по поверхности, соотнесенный с внешней частью поверхности, через тройной интеграл, который берется по самому телу, границей которого является вышеуказанная поверхность.

Следует понимать, что формулы Грина, Стокса и Остроградского выражают интеграл, связанный с некоторым геометрическим телом, через интеграл, который берется на его границе. Формула Грина используется только в случае двумерности пространства, формула Стокса - к искривленному двумерному пространству.

Формулу Ньютона-Лейбница можно также рассматривать как некоторый аналог этих формул, но для одномерного пространства.

Применение данной формулы

Пусть в какой-либо незамкнутой области пространства заданы непрерывные функции A, B и C. Взяв любую замкнутую поверхность, находящуюся в данной области и ограничивающую некоторое тело, можно рассмотреть следующий интеграл по поверхности:

Необходимо найти такие значения A, B и C, чтобы при любых x, y и z данный интеграл оказывался равен нулю.

Для этого необходимо использовать формулу Остроградского-Гаусса. Одним из подразумеваемых условий является определенность и непрерывность функций A, B и C и их производных.

Так же требуется специально ввести наиболее данное для данного случая ограничение: и тело, и ограничивающая его поверхность должны содержаться одновременно в конкретной и указанной области, называемую односвязной. Основная его особенность заключается в отсутствии пустого пространства (в том числе и точечного). Таким образом, границей тела будет являться одна и при том единственная поверхность.

После применения формулы возможно получение следующего условия, которое является достаточным:

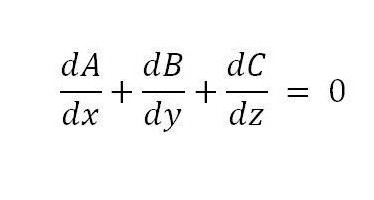
Чтобы доказать, что условие является так же и необходимым, достаточно воспользоваться дифференцированием тройного интеграла.

В заключении необходимо сказать об областях использования.

Как же применяется на практике формула Остроградского-Гаусса? Примеры использования можно обнаружить в самых разных сферах: для вывода некоторых формул в физике (например, уравнение диффузии), преобразования интегралов, вычисления интегралов Гаусса, доказательства некоторых формул и многого иного.