Как рассчитать длину окружности и периметр круга?
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
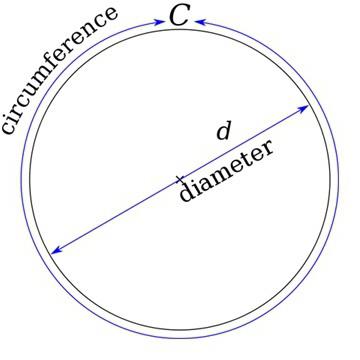
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
До того как рассчитать длину окружности, потребуется договориться о том, какая буква что обозначает. Это удобно записать в таблице.
| Величина | Обозначение |
| радиус | r |
| диаметр | d |
| длина окружности | l |
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
l =2π * r.
Здесь и далее π берется округленным. Чаще всего в задачах используют значение 3,14. Но иногда нужна большая точность и тогда применяют такое число: 3,14159.

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
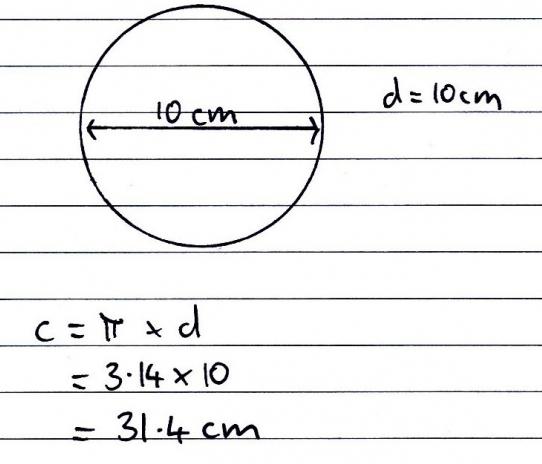
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l1 = 18,84 см, l2= 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Похожие статьи
- Как вычислить диаметр окружности: формула и пояснения
- Как найти длину окружности: через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
- Объем конуса, его расчет
- Как раскроить "солнце" (юбку): расчет, описание, выкройка
- Периметр квадрата и прямоугольника. Способы определения и примеры решения.
- Что представляет собой диаметр окружности
- Цилиндр. Виды, объём цилиндра, площадь поверхности
