Что представляет собой диаметр окружности

Прежде чем рассматривать диаметр окружности, поговорим о ее длине. Под данным термином подразумевают произведение диаметра на число «пи». К примеру, при заданном радиусе круга можно определить не только длину, но и вычислить его площадь. Для любых видов постоянной величиной является дробь, в которой числителем является длина, а знаменатель - это диаметр окружности.

Определение

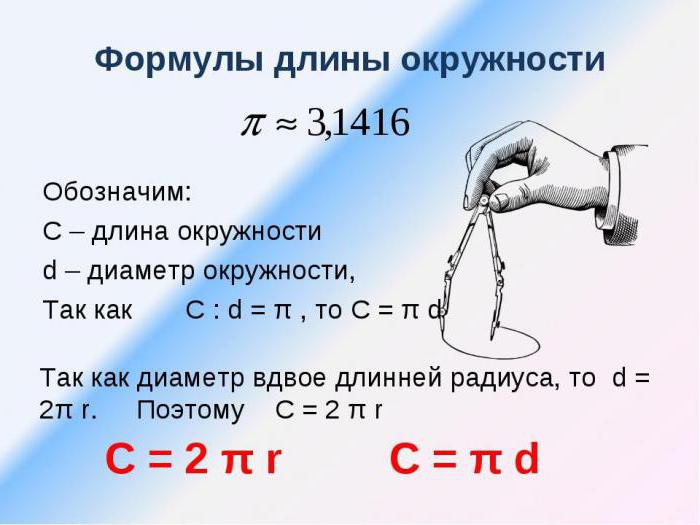
Для всех круглых геометрических фигур одинаковым будет отношение длины к диаметру. Например, зная величину радиуса круглой фигуры, вполне можно найти ее длину, диаметр, а также площадь. Длина круга — это произведение числа "πи" на диаметр окружности.

Такой величиной считают в геометрии кривую линию, ограничивающую круг. Так как фигуры представлены на плоскости, то подобное определение характеризует двухмерное изображение. Точки рассматриваемой кривой на одинаковом расстоянии удалены от центра выбранного круга.

Расчеты

Зная, что представляет собой радиус нашей планеты, несложно определить длину круговой орбиты спутника Земли. На практике проведение подобных вычислений осуществляется редко, так как число «пи» является приблизительным, поэтому высока вероятность погрешности. Для того чтобы определить ее длину в быту через диаметр окружности, используется такой прибор, как курвиметр.

Применение и формула

Зная диаметр окружности, можно осуществлять строительство жилых домов, развлекательных центров, супермаркетов. Инженеры-конструкторы, занимающиеся разработкой разнообразных машин, агрегатов, механизмов, постоянно сталкиваются с подобными вычислениями. Какова формула диаметра данной кривой? Вычерчивают ее с помощью циркуля. В математике применяется прием косвенного вычисления длины окружности.

Самым простым способом является использование радиуса. Диаметр вычисляется как два радиуса. При заданной длине окружности можно определить ее диаметр путем деления длины на число «пи». К примеру, при длине 10 сантиметров диаметр будет составлять 10 : 3,14 = 3,18 сантиметра.

При заданной площади круга, вычисление диаметра проводят путем извлечения квадратного корня из данного числа, затем деления полученного ответа на число «пи». К примеру, при площади круга 25 квадратных сантиметров, квадратный корень составит 5 сантиметров, а после деления этого числа на 3,14, получим 1,59 см. Это и есть диаметр данной в задаче окружности.

Справиться с такими несложными вычислениями может и рядовой ученик школы, и инженер конструкторского бюро.