Адиабатный процесс, его суть и и формулы

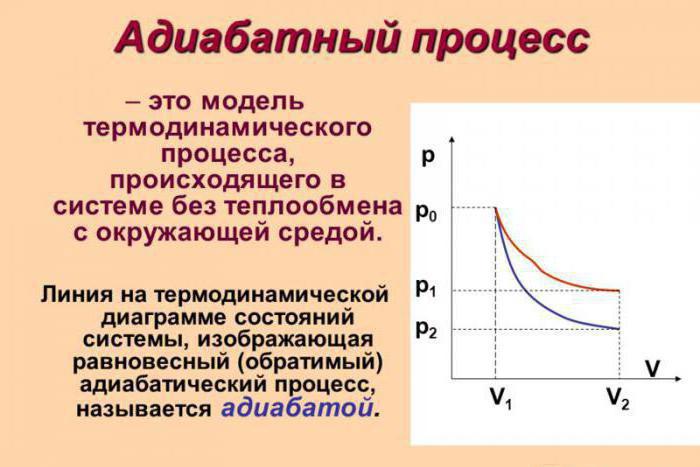
Адиабатный процесс (в некоторых источниках упоминается как адиабатический) - это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.

Связь с первым началом термодинамики

Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.

Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.

В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении. Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю. Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.

Следствие из первого начала термодинамики для адиабатического процесса

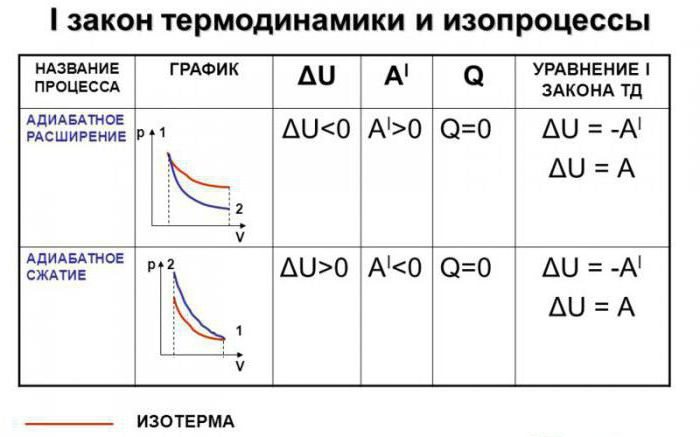
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.

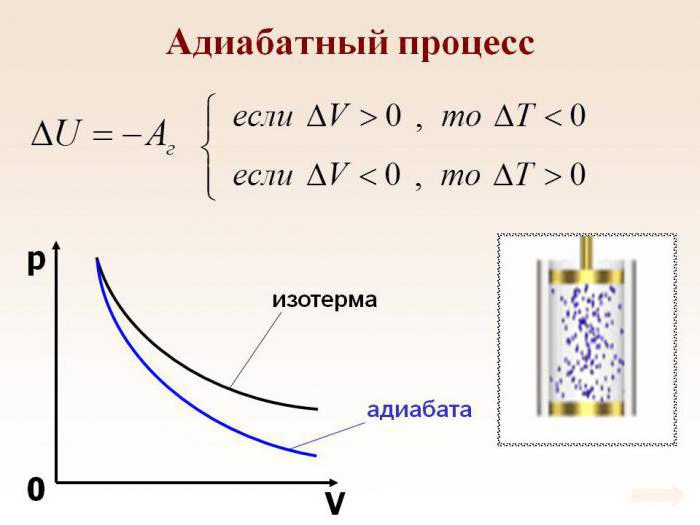
Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.

Адиабатный процесс. Формулы

Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.

Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = - (интеграл) от dU. Раскроем это выражение, получим: A = - xCv (интеграл в пределах от T1 до T2) dT.

Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = - xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).

Уравнение адиабаты

Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.

В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования. Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения. Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.

Первичное выражение

Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp - Cv)

По сути дела, первая часть задачи выполнена. Остается только довести все до ума.

Вторичное выражение. Подстановка значения

Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.

Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю. Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен. В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.

Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.

Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона. Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.

Примеры адиабатных процессов

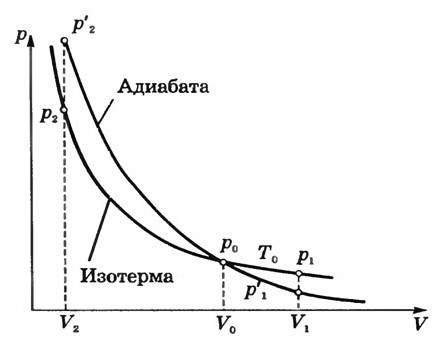
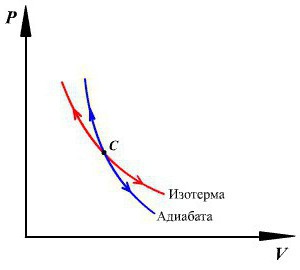
Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.

Заключение

С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике. Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов. Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.